常用激活函数（激励函数）理解和总结
前言最近自己刚刚开始学习神经网络的相关知识，在学习构建一个自定义网络的时候，对于在forward函数中突然出现的Relu函数有点奇怪，然后就去百度查询了一波，原来这就是前面了解概念的时候所说的激活函数也就是激励函数，自己也是在百度和知乎上了解的更加透彻一点点，现在就自己的理解和参考一些别人的说法进行一定的总结，这次总结就主要是如下几点
什么是激活函数
激活函数的作用（为什么就需要激活函数嘞）
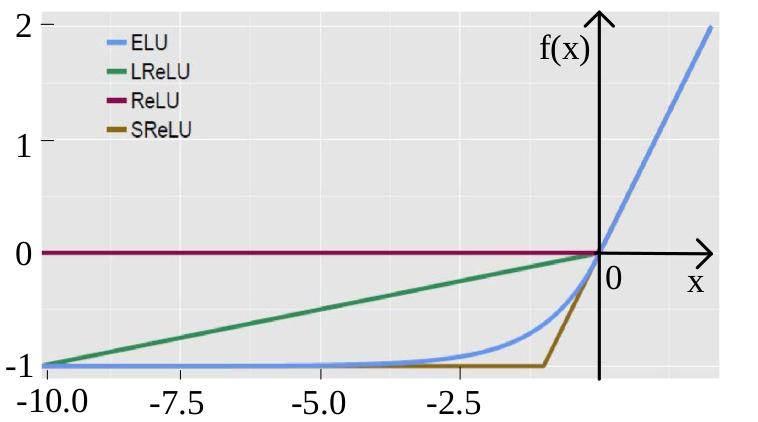
有哪些常用的激活函数，都各自有什么性质和特点
在应用中该如何选择合适的激活函数
什么是激活函数想要了解什么是激活函数，应该先了解神经网络的基本模型，单一的额神经元模型如图1所示。神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值，并将输入值传递给下一层，输入层神经元节点会将输入属性值直接传递给下一层（隐层或输出层）。在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数（又称激励函数）。
图 1 单个神经元结构结构
激活函数的作用查阅了相关资料和学习，大家普遍对神经网络中的激活函数的额作用主要集中在下面这个观点
激活函数是用来加 ...
神经网络的来龙去脉
神经网络的来龙去脉神经，名呼其曰，就是动物的神经系统，从外界的条件触感和感知到大脑中枢的控制再到控制神经做出一系列的反应。
其实，在人工只能领域的神经网络而言，大部分的神经网络都可以用深度 （depth），和连接结构（connection），但是具体的会具体说明。笼统的说，神经网络是可以分为有监督，无监督，半监督的神经网络，其实在这个分类下，忘忘也是你中有我我中有你的的一个局面，在学习的过程中有时候不必要去抠字眼。下面自己在浏览学习后，对神经网络的一点总结。
发展历程：
感知机 ==》多层感知机 ==》深度神经网络 ==》卷积神经网络
神经网络神经网络即指人工神经网络，或称作连接模型，它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。神经网络用到的算法是向量乘法，采用符号函数及其各种逼近。并行、容错、可以硬件实现以及自我学习特性，是神经网络的几个基本优点，也是神经网络计算方法与传统方法的区别所在。
神经网络发展感知机神经网络技术起源于上世纪五、六十年代，当时叫感知机（per ...
马在棋盘上的概率
题意
大意的意思就是在一个棋盘上，马按照象棋中马走日的规则，可以选择走K此后，最后还是留在棋盘的概率。
分析
首先一匹马在任意位置可以选择八个方向走动，称之为方向向量，分别为
12int[] dx = {-2, -1, 1, 2, 2, 1, -1, -2}; //方向导向数组int[] dy = {1, 2, 2, 1, -1, -2, -2, -1};
其次由于棋盘是有限的，所以如果选择的步伐超出了棋盘，则视为无效。
现在给个例子，模拟一下其的走动方位，N=4，k=3，r=0，c=0
1、一开始的时候，这匹马所在的位置
2、走第一步的时候后可以选择的落脚点：只有两个方向是可以选择的呢，其余的都是超出了棋盘的范围
走完第一步后的矩阵如下：
3、仿照上述过程，第二步的走向如下
走完第二步后的矩阵如下：
最长递增子序列
动态规划—两道有趣的题目one：eetcode 300最长递增子序列https://leetcode-cn.com/problems/longest-increasing-subsequence/submissions/
1、题目大意
2、分析看到题目，判断某一个数组的最长递增子序列，注意并不是连续的。
3、方法1：完全递归
现在假设下标 i 结尾的数组的最唱递增子序列为 max，
若nums[i+1]>nums[i] ; 则下标 i+1 结尾的数组的最唱递增子序列为 max+1，否则为 max
所以这个题目是可以拆解子问题的，有子问题最后堆砌到最终答案
设 函数 fun(n,nums) : 表示在数组nums下，以n作为下标的最大递增序列
得到递归方程 ：fun(n,nums) = fun(j,nums)+1 其中 0<=j<i 并且 dp[j]<dp[i] j为【0，i】里面的任意值，需要遍历
拿下图为递归树（简约哈）
代码：
123456789101112131415161718192021222324252627282930313233 ...
BFS和DFS模板
首先，总结一定的模板做题是十分有作用的，善于总结才是我们加强算法能力的表现。做总结可以提高我们的代码能力，可以比较快速解决算法问题，也会更加清晰算法的流程！！十分有必要！！
BFS的模板：
1、如果不需要确定当前遍历到了哪一层，BFS 模板如下。
12345while queue 不空： cur = queue.pop() for 节点 in cur的所有相邻节点： if 该节点有效且未访问过： queue.push(该节点)
2、如果要确定当前遍历到了哪一层，BFS 模板如下。 这里增加了 level 表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。size 表示在当前遍历层有多少个元素，也就是队列中的元素数，我们把这些元素一次性遍历完，即把当前层的所有元素都向外走了一步。
12345678910level = 0while queue 不空： size = queue.size() while (size --) { cur = queue.pop() ...
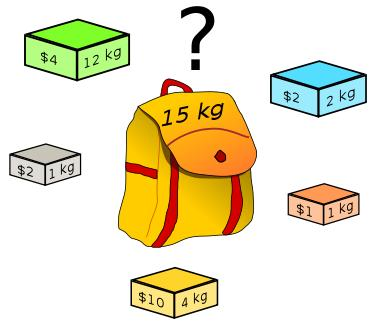
背包问题
动态规划动态规划（Dynamic Programming，简称DP）动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再合并子问题的解以得出原问题的解。 通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量： 一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。虽然抽象后进行求解的思路并不复杂，但具体的形式千差万别，找出问题的子结构以及通过子结构重新构造最优解的过程很难统一，为了解决动态规划问题，只能靠多练习、多思考了。
\动态规划问题满足三大重要性质**
最优子结构性质：如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
子问题重叠性质：子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新 ...
编程中无穷大常量(ox3f3f3f3f)的设定技巧
编程中无穷大常量的设定技巧首先，在做某一些算法的时候，会很常求最大最小值一类的问题，通常我们会设置一个初始一个answer最大int类型的最大或者最小，然后每次比较取大取小即可。
其实如果问题中各数据的范围明确，那么无穷大的设定不是问题，在不明确的情况下，很多程序员都取0x7fffffff作为无穷大，因为这是32-bit int的最大值。如果这个无穷大只用于一般的比较（比如求最小值时min变量的初值），那么0x7fffffff确实是一个完美的选择，但是在更多的情况 下，0x7fffffff并不是一个好的选择。理由如下：
很多时候我们并不只是单纯拿无穷大来作比较，而是会运算后再做比较，例如在大部分最短路径算法中都会使用的松弛操作：if (d[u]+w[u][v]<d[v]) d[v]=d[u]+w[u][v];我们知道如果u,v之间没有边，那么w[u][v]=INF，如果我们的INF取0x7fffffff，那么d[u]+w[u][v]会溢出而变成负数， 我们的松弛操作便出错了，更一般的说，0x7fffffff不能满足“无穷大加一个有穷的数依然是无穷大”，它变成了一个很小的负数。
计 ...
tcp详解
1、tcp协议的特点TCP是在不可靠的IP层之上实现的可靠的数据传输协议，它主要解决传输的可靠、有序、无丢失和不重复问题。TCP 是TCP/IP 体系中非常复杂的一个协议，主要特点如下：
TCP 是面向连接的传输层协议。
每条TCP 连接只能有两个端点，每条TCP 连接只能是点对点的（一对一）。
TCP 提供可靠的交付服务，保证传送的数据无差错、不丢失、不重复且有序。
如何保证数据无差错、不丢失、不重复且有序的？有哪些机制来保证？
答：TCP 使用了校验、序号、确认和重传等机制来达到这一目的。
TCP 提供全双工通信，允许通信双方的应用进程在任何时候都能发送数据，为此TCP 连接的两端都设有发送缓存和接收缓存，用来临时存放双向通信的数据。
为什么需要设置缓存，缓存的作用？
答：发送缓存用来暂时存放以下数据：1.发送应用程序传送给发送方TCP 准备发送的数据；2.TCP已发送但尚未收到确认的数据。
接收缓存用来暂时存放以下数据：1.按序到达但尚未被接收应用程序读取的数据；2.不按序到达的数据。
TCP是面向字节流的，虽然应用程序和TCP的交互是一次一个数据块（大小 ...
Hello World
Welcome to Hexo! This is your very first post. Check documentation for more info. If you get any problems when using Hexo, you can find the answer in troubleshooting or you can ask me on GitHub.
Quick StartCreate a new post1$ hexo new "My New Post"
More info: Writing
Run server1$ hexo server
More info: Server
Generate static files1$ hexo generate
More info: Generating
Deploy to remote sites1$ hexo deploy
More info: Deployment
