常用卷积总结

符号约定

输入：$H_{in} \times W_{in} \times C_{in}$，其中 $H_{in}$ 为输入 feature map的高，$W_{in}$ 为宽，$C_{in}$ 为通道数
输出：$H_{out} \times W_{out} \times C_{out}$，其中 $H_{out}$ 为输入 feature map的高，$W_{out}$ 为宽，$C_{out}$ 为通道数
卷积核：$N \times K \times K \times C_k$ ，其中 N 为该卷积层的卷积核个数，$K$ 为卷积核宽与高(默认相等)，$C_k$ 为卷积核通道数

常规卷积

特点：

卷积和通道数与输入 feature map的通道数相等，即 $C_{in} = C_k$
输出 feature map 的通道数等于卷积核的个数，即 $C_{out} = N$

卷积过程：

卷积核在输入 feature map 中移动，按位点乘后求和即可，通道也会求和。

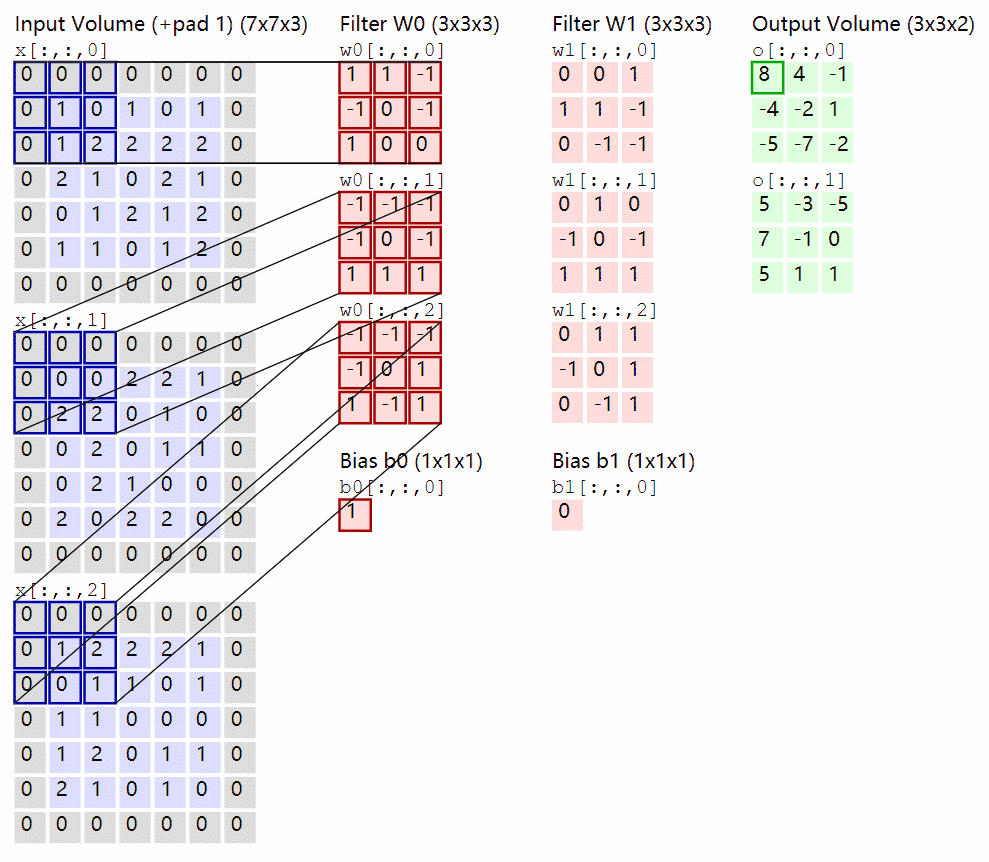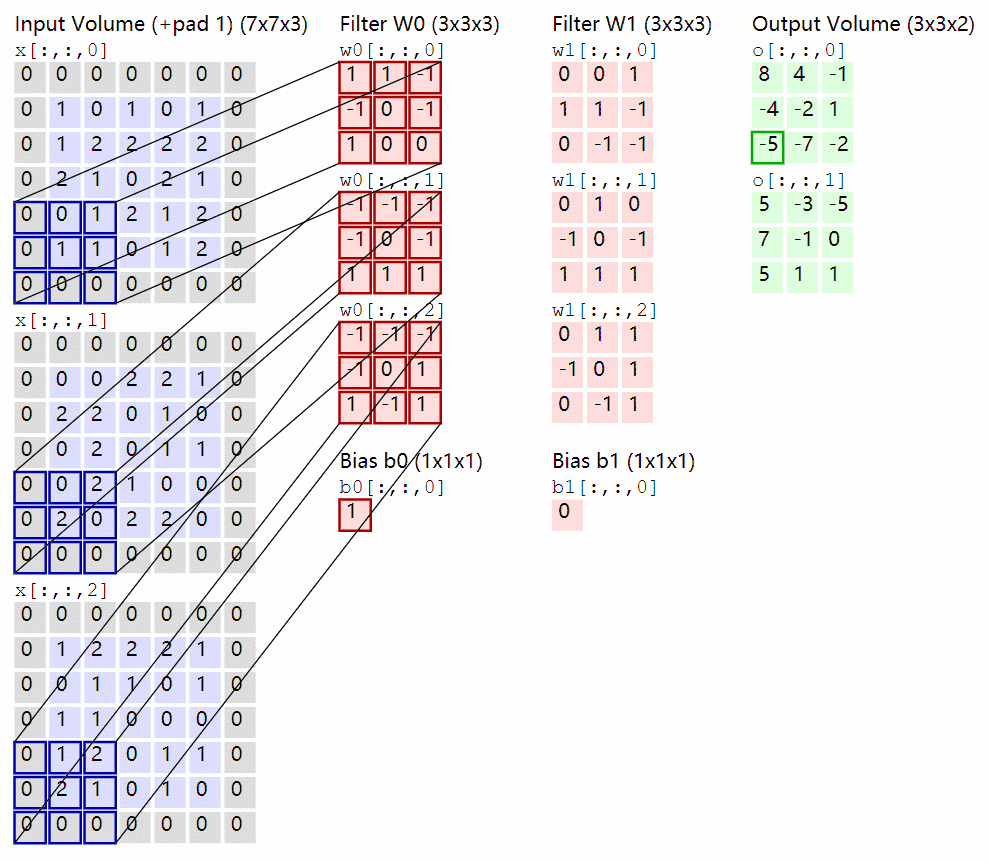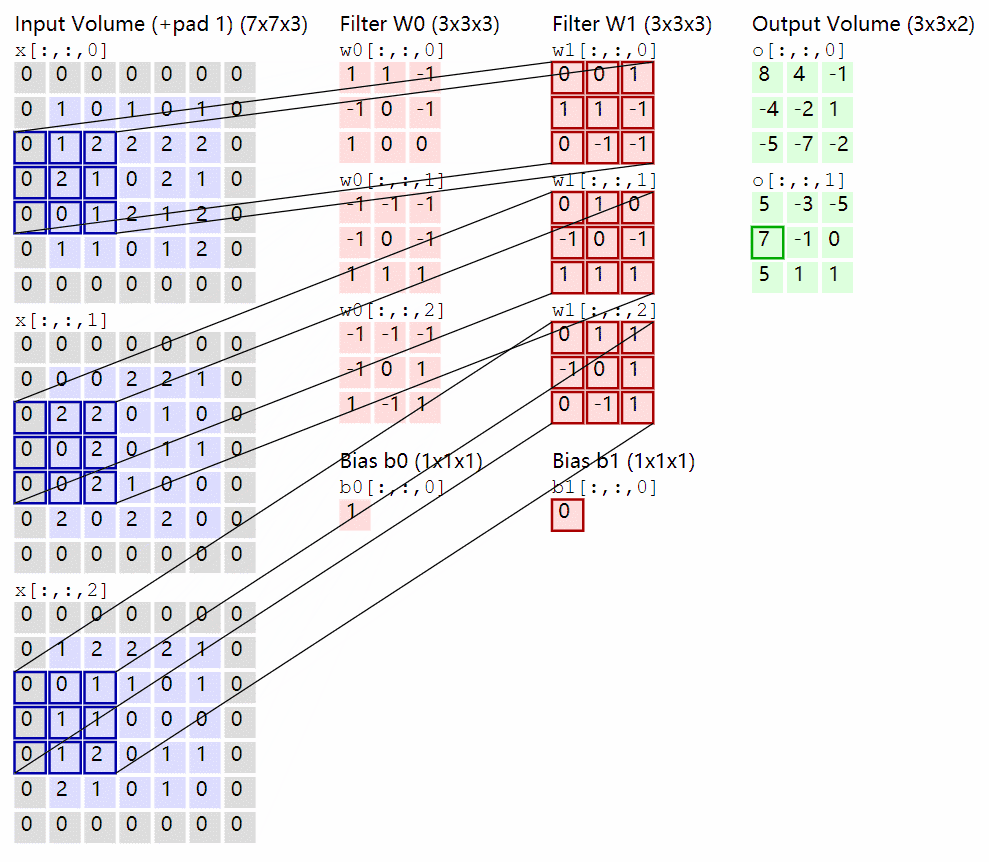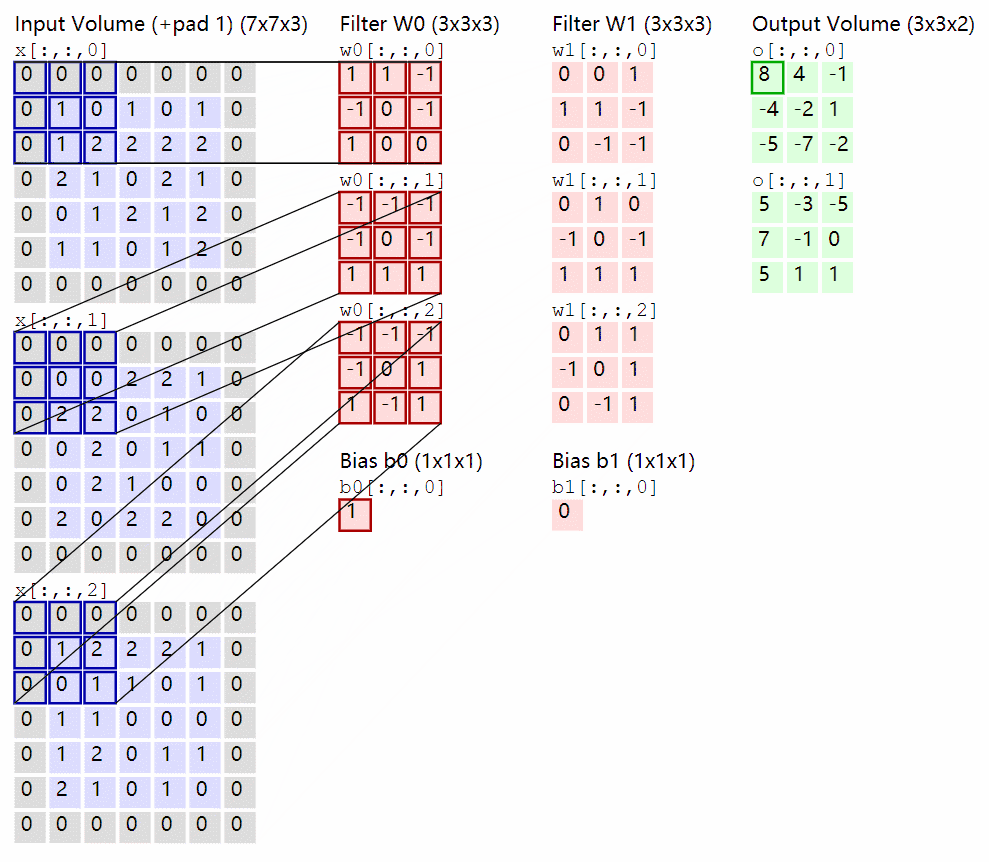
函数语法格式，二维卷积最常用的卷积方式，先实例化再使用。

1	nn. Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode= 'zeros' )

参数解释
- in_channels ：输入的四维张量[N, C, H, W]中的C，也就是说输入张量的channels数。这个形参是确定权重等可学习参数的shape所必需的。
- out_channels：即是期望的输出四维张量的channels数。
- kernel_size ：卷积核的大小，一般我们会使用 5x5、3x3 这种左右两个数相同的卷积核，因此这种情况只需要写kernel_size = 5这样的就行了。如果左右两个数不同，比如3x5的卷积核，那么写作kernel_size = (3, 5)，注意需要写一个tuple，而不能写一个列表（list）。
- stride = 1：卷积核在图像窗口上每次平移的间隔，即所谓的步长。跟Tensorflow框架等的意义一样。
- padding=0：padding也就是指图像填充，后面的int型常数代表填充的多少（行数、列数），默认为0。需要注意的是这里的填充包括图像的上下左右，以padding=1为例，若原始图像大小为32*32，那么padding后的图像大小就变成了 34*34，而不是33*33。这是Pytorch与Tensorflow在卷积层实现上最大的差别。
- dilation=1：这个参数决定了是否采用空洞卷积，默认为1（不采用）。从中文上来讲，这个参数的意义从卷积核上的一个参数到另一个参数需要走过的距离，那当然默认是1了，毕竟不可能两个不同的参数占同一个地方吧（为0）
- groups=1：决定了是否采用分组卷积，默认值为 1 .
- bias=True ：即是否要添加偏置参数作为可学习参数的一个，默认为True。
- padding_mode ：即padding的模式，默认采用零填充。
输出图像的计算公式
- 在大多数情况下，大多数情况下的 kernel_size、padding左右两数均相同，且不采用空洞卷积（dilation默认为1），因此只需要记住这种在深度学习课程里学过的公式就好了。
  $O = \frac{I-K+2P}{S} + 1$

1X1卷积

特点、作用：

顾名思义，卷积核大小为 1ｘ1
卷积核通道数与输入 feature map 的通道数相等，即 $C_{in} = C_k$
输出 feature map 的通道数等于卷积核的个数，即 $C_{out} = N$
不改变 feature map 的大小，目的是为了改变 channel 数，即 1ｘ1 卷积的使用场景是：不想改变输入 feature map 的宽高，但想改变它的通道数。即可以用于升维或降维。
相比 3ｘ3 等卷积，计算量及参数量都更小，计算量和参数量的计算参考另一篇文章 (22_CNN网络各种层的FLOPs和参数量paras计算)
加入非线性。1*1的卷积在不同 channels 上进行线性整合，在前一层的学习表示上添加了非线性激励（ non-linear activation ），提升网络的表达能力；

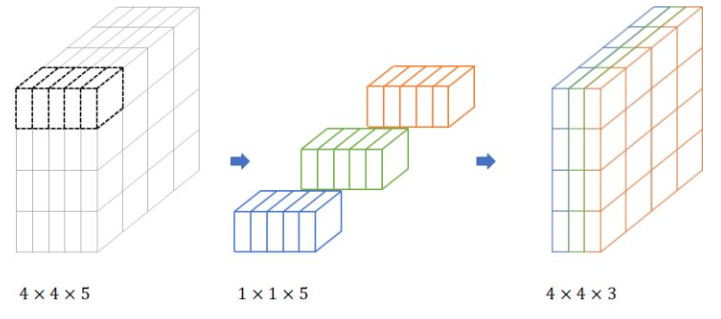
1x1核的主要目的是应用非线性。在神经网络的每一层之后，我们都可以应用一个激活层。无论是ReLU、PReLU、Sigmoid还是其他，与卷积层不同，激活层是非线性的。非线性层扩展了模型的可能性，这也是通常使“深度”网络优于“宽”网络的原因。为了在不显著增加参数和计算量的情况下增加非线性层的数量，我们可以应用一个1x1内核并在它之后添加一个激活层。这有助于给网络增加一层深度

分组卷积（Group Convolution）

Group convolution 分组卷积，最早在 AlexNet 中出现，由于当时的硬件资源有限，训练 AlexNet 时卷积操作不能全部放在同一个 GPU 处理，因此作者把 feature maps 分给多个GPU分别进行处理，最后把多个 GPU 的结果进行融合。

卷积过程

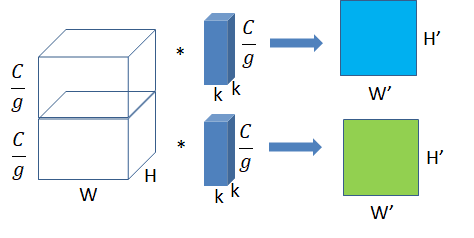
将输入 feature map 分成 g 组，一个卷积核也相对应地分成 g 组，在对应的组内做卷积。（我们可以理解成分组卷积中使用的 g 组卷积核整体对应于常规卷积中的一个卷积核，只不过是将常规卷积中的一个卷积核分成了 g 组而已）

特点、作用：

输入的 feature map 尺寸：$H_{in}W_{in} \frac{C_{in}}{g}$ ，共有 g 组
卷积核的规格：$NKK\frac{C_{k}}{g}$，共有 N g 组
输出 feature map 规格：$H_{out}W_{out}Ng$ ，共生成 Ng 个 feature map
当 g=1 时就退化成了上面讲过的常规卷积，当 $g=C_{in}$ 时就是我们下面将要讲述的深度分离卷积。
用常规卷积得到一个输出 feature map 的计算量和参数量便可以得到 g 个输出 feature map，所以分组卷积常用在轻量型高效网络中，因为它可以用少量的参数量和计算量生成大量的 feature map。
优点
- 标准2D卷积参数量：$W \times H \times C_{in} \times C_k$
- 分组卷积参数量：$W \times H \times C_{in}/2 \times C_k/2 \times 2$
- group=2,参数量减少到原来的1/2；group=4,参数量减少到原来的1/4；总结：参数量减少1/g。
- 减少运算量和参数量，相同输入输出大小的情况下，减少为原来的 1/g
代码的话很简单，就是 nn.Conv2d 里面的一个参数：group。

可分离卷据（Separable Convolution）

空间可分离卷积

之所以命名为空间可分离卷积，是因为它主要处理的是卷积核的空间维度：宽度和高度。

空间可分离卷积简单地将卷积核划分为两个较小的卷积核。最常见的情况是将3x3的卷积核划分为3x1和1x3的卷积核，如下所示：

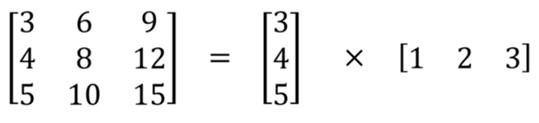
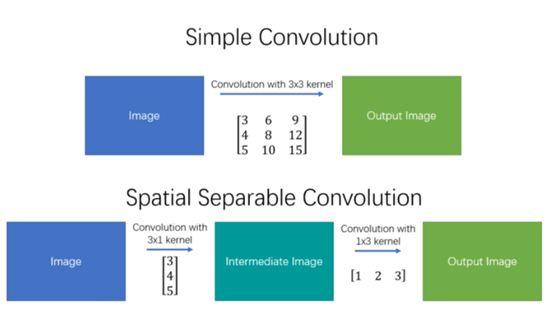
局限性：并不是所有的卷积核都可以“分离”成两个较小的卷积核，==能够“分离”的是那些卷积核参数大小的行和列有一定倍数关系的==. 这在训练期间变得特别麻烦，因为网络可能采用所有可能的卷积核，它最终只能使用可以分成两个较小卷积核的一小部分。所以实际中用的不多
参数量和计算量更少：如上图所示，不是用9次乘法进行一次卷积，而是进行两次卷积，每次3次乘法（总共6次），以达到相同的效果。乘法较少，计算复杂性下降，网络运行速度更快。

深度可分离卷积（Depthwise Separable Convolution）

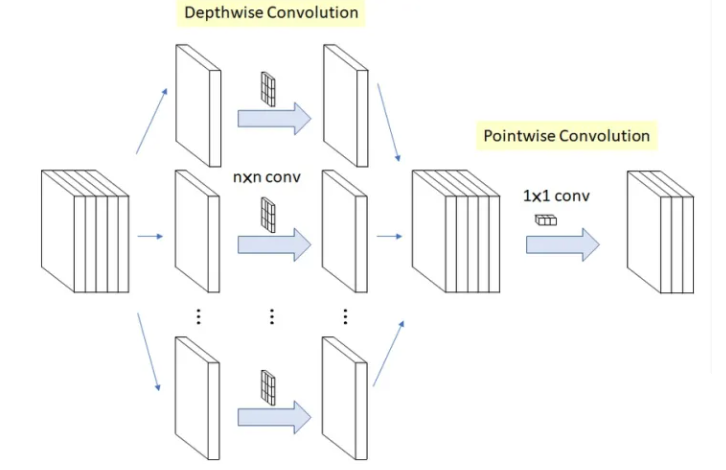
深度可分离卷积的过程分为两个部分：深度卷积（depthwise convolution）和逐点卷积（pointwise convolution）

（1）深度卷积

深度卷积意在保持输入 feature map 的通道数，即对 feature map 中的每个通道使用一个规格为 $KK1$ 的卷积核进行卷积，于是输入 feature map 有多少个通道就有多少个这样的卷积核，深度卷积结束后得到的输出的通道数与输入的相等。

Depthwise Convolution的一个卷积核负责一个通道，一个通道只被一个卷积核卷积，这个过程产生的feature map通道数和输入的通道数完全一样。

这一步其实就相当于常规卷积中的一个卷积核，只不过不同通道的卷积结果不相加而已，自己体会体会。

Depthwise Convolution完成后的Feature map数量与输入层的通道数相同，无法扩展Feature map。而且这种运算对输入层的每个通道独立进行卷积运算，没有有效的利用不同通道在相同空间位置上的feature信息。因此需要Pointwise Convolution来将这些Feature map进行组合生成新的Feature map。

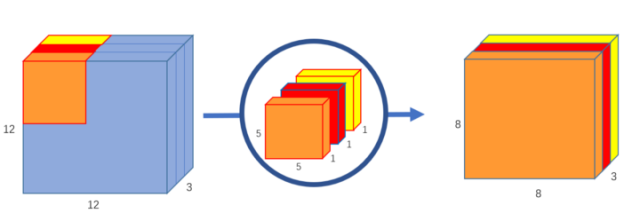
（2）逐点卷积

在上一步的基础上，运用 1ｘ1 卷积进行逐点卷积。

使用一个 1ｘ1 卷积核就可以得到输出 feature map 一维的结果。

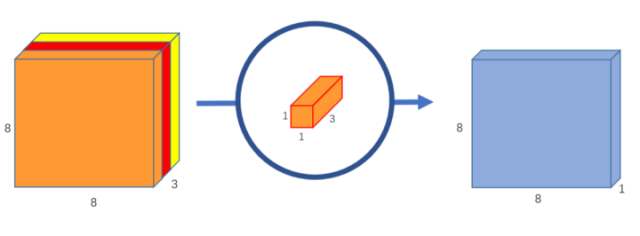
如果你要输出 feature map 有 256 维，那么就使用 256 个 1ｘ1 卷积核即可。

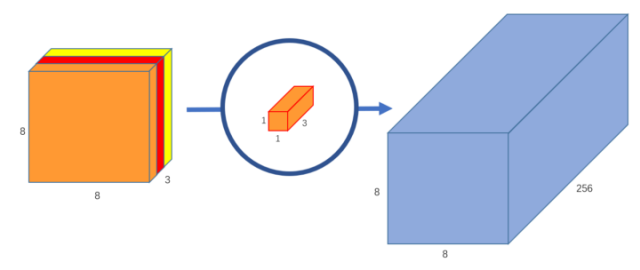
可以理解成常规的卷积分成了两步执行，但是分成两步后参数量和计算量大大减少，网络运行更快
深度分离卷积几乎是构造轻量高效模型的必用结构，如Xception, MobileNet, MobileNet V2, ShuffleNet, ShuffleNet V2, CondenseNet等轻量型网络结构中的必用结构。

转置卷积（Transposed Convolution）

转置卷积（Transposed Convolution） 在语义分割或者对抗神经网络（GAN）中比较常见，其主要作用就是做上采样。

转置卷积不是卷积的逆运算、不是逆运算、不是逆运算（重要的事情说三遍）
转置卷积也是卷积

函数语法格式：

1	torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, bias=True)

概述：就是反卷积，该函数是用来进行转置卷积的，它主要做了这几件事：首先，对输入的feature map进行padding操作，得到新的feature map；然后，随机初始化一定尺寸的卷积核；最后，用随机初始化的一定尺寸的卷积核在新的feature map上进行卷积操作。卷积核确实是随机初始的，但是后续可以对卷积核进行单独的修改

主要作用就是起到上采样的作用。但转置卷积不是卷积的逆运算（一般卷积操作是不可逆的），它只能恢复到原来的大小（shape），数值与原来不同。转置卷积的运算步骤可以归为以下几步：

1、在输入特征图元素间填充 stride-1 行列 0（其中 stride 表示转置卷积的步距）
2、在输入特征图四周填充 k-p-1 行列0（其中k表示转置卷积的kernel_size大小，p为转置卷积的padding，注意这里的padding和卷积操作中有些不同）
3、将卷积核参数上下、左右翻转
4、做正常卷积运算（填充0，步距1）

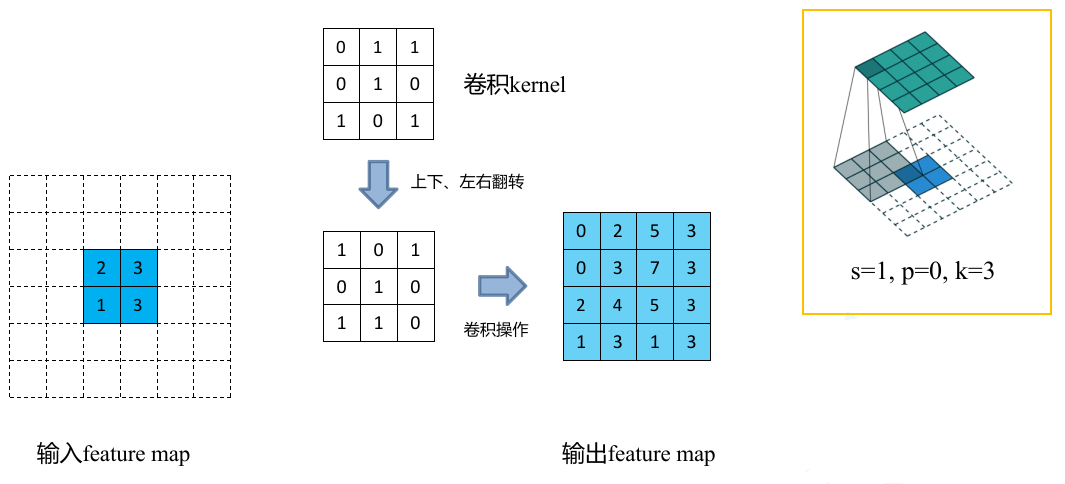
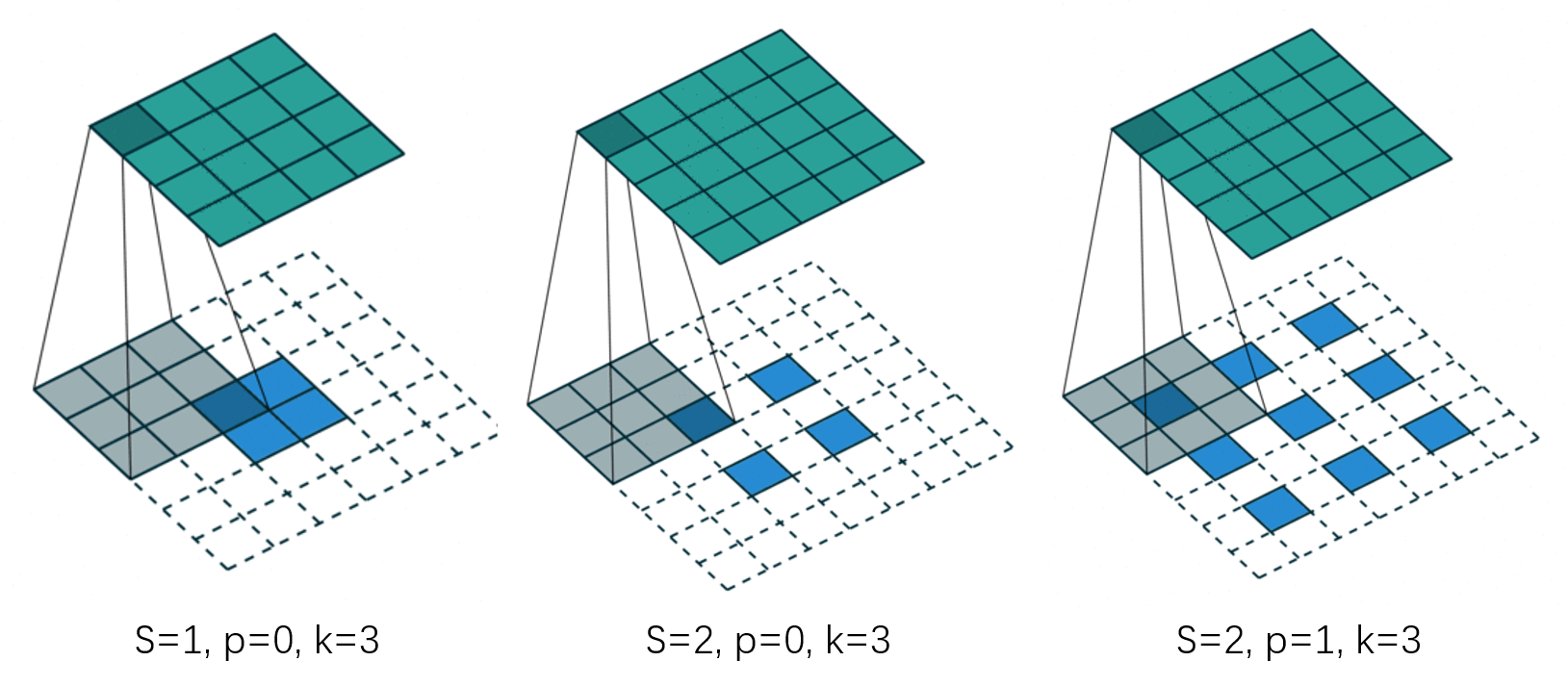
下图展示了转置卷积中不同 stride 和 padding 的情况：

输出尺寸计算：

$output = (input-1) * stride + output\_padding - 2*padding + kernel_size$

不过时常 output_padding=0,

$output = (input-1) * stride - 2*padding + kernel_size$

空洞卷积（Dilated Convolution）

空洞卷积也叫扩张卷积或者膨胀卷积，简单来说就是在卷积核元素之间加入一些空格(零)来扩大卷积核的过程。

空洞卷积诞生在图像分割领域，在一般的卷积结构中因为存在 pooling 操作，目的是增大感受野也增加非线性等，但是 pooling 之后特征图的大小减半，而图像分割是 pixel-wise 的，因此后续需要 upsamplng 将变小的特征图恢复到原始大小，这里的 upsampling 主要是通过转置卷积完成，但是经过这么多的操作之后会将很多细节丢失，那么空洞卷积就是来解决这个的，既扩大了感受野，又不用 pooling 。

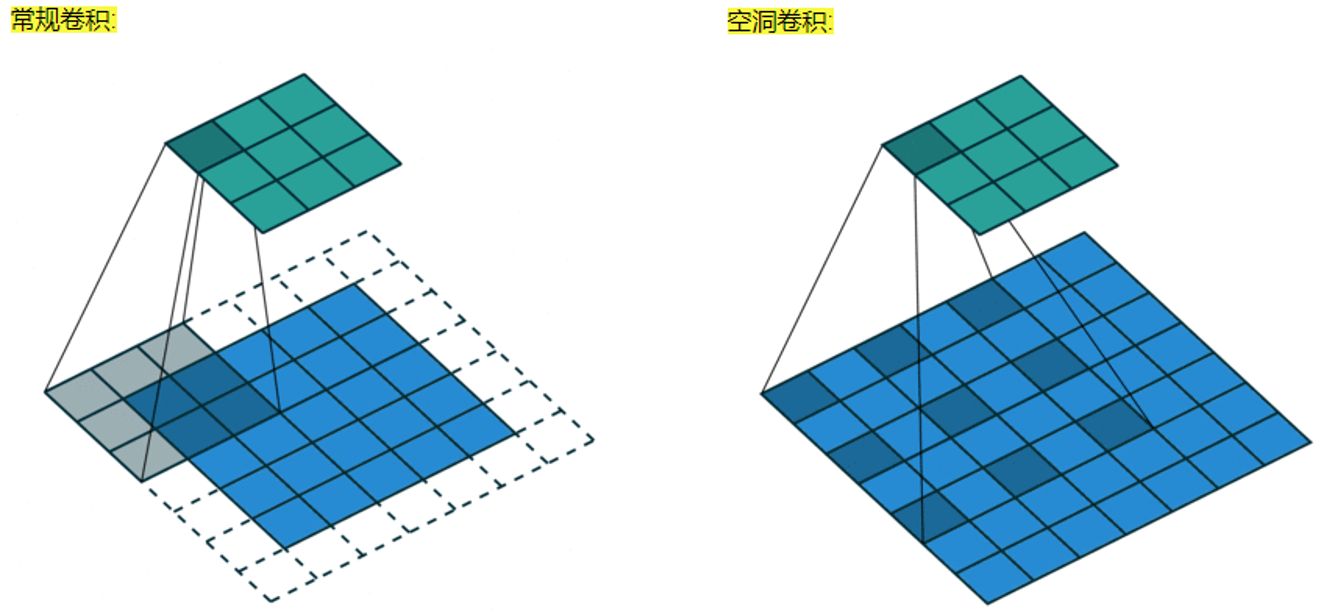
假设以一个变量a来衡量空洞卷积的扩张系数，则加入空洞之后的实际卷积核尺寸与原始卷积核尺寸之间的关系：K = K + (k-1)(a-1)

其中k为原始卷积核大小，a为卷积扩张率(dilation rate)，K为经过扩展后实际卷积核大小。除此之外，空洞卷积的卷积方式跟常规卷积一样。我们用一个扩展率a来表示卷积核扩张的程度。比如说a=1,2,4的时候卷积核核感受野如下图所示：

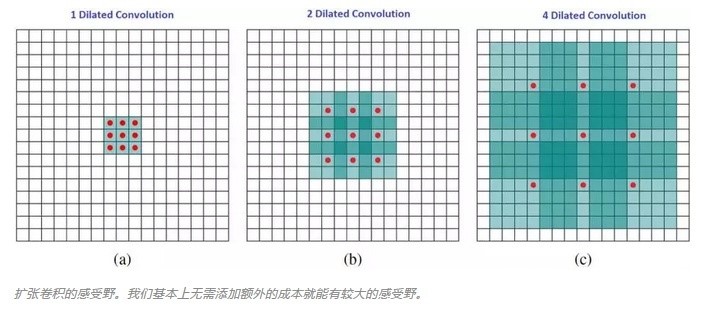
在这张图像中，3×3 的红点表示经过卷积后，输出图像是 3×3 像素。尽管所有这三个扩张卷积的输出都是同一尺寸，但模型观察到的感受野有很大的不同。当a=1，原始卷积核size为3 3，就是常规卷积。a=2时，加入空洞之后的卷积核：size=3+(3-1) (2-1)=5，对应的感受野可计算为：(2 ^(a+2))-1=7。a=3时，卷积核size可以变化到3+(3-1)(4-1)=9，感受野则增长到 (2 ^(a+2))-1=15。有趣的是，与这些操作相关的参数的数量是相等的。我们「观察」更大的感受野不会有额外的成本。因此，扩张卷积可用于廉价地增大输出单元的感受野，而不会增大其核大小，这在多个扩张卷积彼此堆叠时尤其有效。

扩大感受野：一般来说，在深度神经网络中增加感受野并且减少计算量的方法是下采样。但是下采样牺牲了空间分辨率和一些输入的信息。空洞卷积一方面增大了感受野可以检测分割大目标，另一方面相较于下采样增大了分辨率可以精确定位目标。
捕获多尺度上下文信息：当设置不同dilation rate时，感受野就会不一样，也即获取了多尺度信息。
代码实现就是控制 nn.Conv2d 里面的一个参数：dilation 。