常见代码实现
Softmax
计算公式:
计算过程:
- 对每个项求幂(使用exp;
torch.exp()) - 对每一行(某一维度)求最大值,并且该行(维度)的值减去最大值,否则求exp(x)可能会溢出,导致inf的情况;
- 对每一行(某一维度)求和,得到每个样本的规范化常数。
- 将每一行除以其规范化常数,确保结果的和为1。
- 对每个项求幂(使用exp;
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31# numpy
def softmax(x, axis=1):
# 计算每行的最大值
# row_max = x.max(axis=axis)
# row_max = np.expand_dims(row_max, axis=axis)
row_max = np.max(x, axis=axis, keepdims=True)
# 每行元素都需要减去对应的最大值,否则求exp(x)会溢出,导致inf情况
x = x - row_max
# 计算e的指数次幂
x_exp = np.exp(x)
x_sum = np.sum(x_exp, axis=axis, keepdims=True)
s = x_exp / x_sum
return s
# pytorch
def softmax1(x, dim=1):
# 计算每行的最大值
# 1、不保留后恢复
# row_max, _ = torch.max(x, dim=dim);
# row_max = row_max.unsqueeze(dim) # 恢复一个为1维度,方便广播机制
# 2、保留维度
row_max, _ = torch.max(x, dim=dim, keepdims=True);
# 每行元素都需要减去对应的最大值,否则求exp(x)会溢出,导致inf情况
x = x - row_max # 广播机制
# 计算e的指数次幂
x_exp = torch.exp(x)
x_sum = torch.sum(x_exp, dim=dim, keepdims=True)
s = x_exp / x_sum # 广播机制
return s
Sigmoid
计算公式:
代码:直接套公式
1
2
3
4
5
6
7# numpy
def sigmoid(x):
return 1.0 / (1 + np.exp(-x))
# pytorch
def sigmoid(x):
return 1.0 / (1 + torch.exp(-x))
CrossEntropy
计算公式:
代码:
1
2
3
4
5
6
7
8# y是one-hot编码
def cross_entropy_error(p,y):
assert y.shape == p.shape # 判读shape是否一致
delta=1e-7 #添加一个微小值可以防止负无限大(np.log(0))的发生。
p = softmax(p) # 通过 softmax 变为概率分布,并且sum(p) = 1
# return -np.sum( y * np.log(p+delta) ) 多分类
# return -(y * np.log(p) + (1 - y) * np.log(1 - p)) 二分类
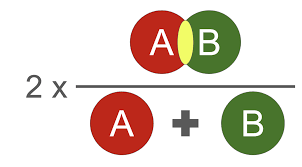
mDice
- 计算公式:
代码实现:
1
2
3
4
5
6
7
8# H*W
def dice_coeff(pred, target):
smooth = 1.
num = pred.size(0)
m1 = pred.view(num, -1) # Flatten
m2 = target.view(num, -1) # Flatten
intersection = (m1 * m2).sum() # 计算交集
return (2. * intersection + smooth) / (m1.sum() + m2.sum() + smooth)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39# H*W
def dice_coeff(input: Tensor, target: Tensor, reduce_batch_first: bool = False, epsilon=1e-6):
# Average of Dice coefficient for all batches, or for a single mask
assert input.size() == target.size()
if input.dim() == 2 and reduce_batch_first:
raise ValueError(f'Dice: asked to reduce batch
but got tensor without batch dimension (shape {input.shape})')
if input.dim() == 2 or reduce_batch_first:
inter = torch.dot(input.reshape(-1), target.reshape(-1))
sets_sum = torch.sum(input) + torch.sum(target)
if sets_sum.item() == 0:
sets_sum = 2 * inter
return (2 * inter + epsilon) / (sets_sum + epsilon)
else:
# compute and average metric for each batch element
dice = 0
for i in range(input.shape[0]):
dice += dice_coeff(input[i, ...], target[i, ...])
return dice / input.shape[0]
def multiclass_dice_coeff(input: Tensor, target: Tensor,
reduce_batch_first: bool = False, epsilon=1e-6):
# Average of Dice coefficient for all classes
assert input.size() == target.size()
dice = 0
for channel in range(input.shape[1]):
dice += dice_coeff(input[:, channel, ...], target[:, channel, ...],
reduce_batch_first, epsilon)
return dice / input.shape[1]
def dice_loss(input: Tensor, target: Tensor, multiclass: bool = False):
# 在调用的时候,groud-truth若是多类别,需要进行one-hot编码
# 【B,C,H,W】target and input
# Dice loss (objective to minimize) between 0 and 1
assert input.size() == target.size()
fn = multiclass_dice_coeff if multiclass else dice_coeff
return 1 - fn(input, target, reduce_batch_first=True)
mIoU
公式:简单来说就是: 交集/并集
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41# 输入 pred,target 【B,H,W】
# 第一种方式 比较合适我理解
def iou_mean(pred, target, n_classes = 1):
# n_classes :the number of classes in your dataset,not including background
# for mask and ground-truth label, not probability map
ious = [] #每个类别的 IoU
iousSum = 0
pred = pred.view(-1)
target = target.view(-1)
# Ignore IoU for background class ("0")
for cls in range(1, n_classes+1):
pred_inds = pred == cls
target_inds = target == cls
# Cast to long to prevent overflows
intersection = (pred_inds[target_inds]).long().sum().data.cpu().item()
union = pred_inds.long().sum().data.cpu().item() +
target_inds.long().sum().data.cpu().item() - intersection
if union == 0:
ious.append(float('nan')) # If there is no ground truth, do not include in evaluation
else:
ious.append (float(intersection) / float(max(union, 1)))
iousSum += float(intersection) / float(max(union, 1))
return iousSum/n_classes # mIoU
# 第二种方式
# 'K' classes, output and target sizes are N or N * L or N * H * W, each value in range 0 to K - 1.
def intersectionAndUnion(output, target, K, ignore_index=255):
assert output.ndim in [1, 2, 3]
assert output.shape == target.shape
output = output.reshape(output.size).copy()
target = target.reshape(target.size)
output[np.where(target == ignore_index)[0]] = ignore_index
intersection = output[np.where(output == target)[0]]
area_intersection, _ = np.histogram(intersection, bins=np.arange(K + 1))
area_output, _ = np.histogram(output, bins=np.arange(K + 1))
area_target, _ = np.histogram(target, bins=np.arange(K + 1))
area_union = area_output + area_target - area_intersection
ious = area_intersection / area_union+epsilon # 是一个array,代表每个类别的IoU
mIoU = np.nanmean(ious) # mIoU
Self-Attention
计算公式:
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53impotr torch
from torch import nn
from torch.nn import functional as F
class Attention(nn.Module):
"""
An attention layer that allows for downscaling the size of the embedding
after projection to queries, keys, and values.
"""
def __init__(
self,
embedding_dim: int,
num_heads: int,
downsample_rate: int = 1,
attn_drop_ratio=0.,
):
super().__init__()
self.embedding_dim = embedding_dim
self.internal_dim = embedding_dim // downsample_rate
self.num_heads = num_heads
self.attn_drop = nn.Dropout(attn_drop_ratio)
assert self.internal_dim % num_heads == 0, "num_heads must divide embedding_dim."
self.q_proj = nn.Linear(embedding_dim, self.internal_dim)
self.k_proj = nn.Linear(embedding_dim, self.internal_dim)
self.v_proj = nn.Linear(embedding_dim, self.internal_dim)
self.out_proj = nn.Linear(self.internal_dim, embedding_dim)
def forward(self, q, k, v): # [B,N,C]
# Input projections
q = self.q_proj(q) # [B,N,C1]
k = self.k_proj(k)
v = self.v_proj(v)
# Separate into heads
b, n, c = q.shape
q = q.reshape(b, n, self.num_heads, c // self.num_heads).transpose(1, 2) # [B, N_heads, N_tokens, C_per_head]
k = k.reshape(b, n, self.num_heads, c // self.num_heads).transpose(1, 2) # [B, N_heads, N_tokens, C_per_head]
v = v.reshape(b, n, self.num_heads, c // self.num_heads).transpose(1, 2) # [B, N_heads, N_tokens, C_per_head]
# Attention
_, _, _, c_per_head = q.shape
attn = q @ k.permute(0, 1, 3, 2) # [B, N_heads, N_tokens, N_tokens]
attn = attn / math.sqrt(c_per_head)
attn = torch.softmax(attn, dim=-1)
attn = self.attn_drop(attn)
# Get output
out = attn @ v # [B, N_heads, N_tokens, C_per_head]
out = out.transpose(1, 2).reshape(b, n, self.num_heads * c_per_head) # [B, N_tokens, C]
out = self.out_proj(out)
return out
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 sevenboy!