常见模块的参数量与计算量
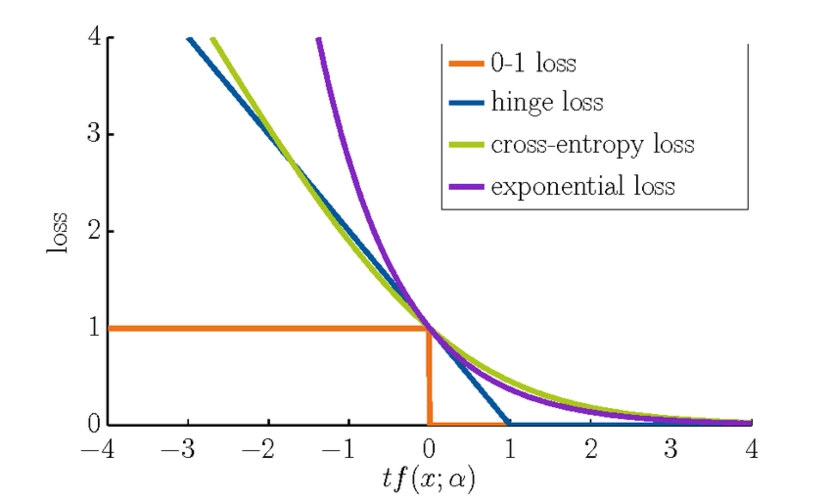
计算量(FLOPs)和参数量(Parameters)
- FLOPS(全大写):是floating point operations per second的缩写,意指每秒浮点运算次数,理解为计算速度,是一个衡量硬件性能的指标。
- FLOPs(s小写):,是floating point operations的缩写(s表复数),意指浮点运算数,理解为计算量,可以用来衡量算法/模型的复杂度,也就是我们这里要讨论的计算量。
- 参数定义(下同):$C_{int}$为输入通道数,k 为卷积核边长, $C_{out}$为输出通道数,$H_{out}*W_{out}$ 为输出特征图的长宽。
- FLOPs = Paras $H_{out}W_{out}$ ;大致是这样的,参数量是和输入特征图大小无关的。
标准卷积层
Parameters:
- 考虑 bias:$(k^2C_{int}+1)C_{out}$
- 不考虑 bias:$(k^2C_{int})C_{out}$
FLOPs:
- 考虑 bias:$(2C_{int}k^2)C_{out}H_{out}*W_{out}$
- 不考虑 bias:$(2C_{int}k^2-1)C_{out}H_{out}*W_{out}$
其实卷积层在实现的时候可以选择加bias或者不加,在很多的框架当中是一个可以选择的参数,为了严谨,这里特地提一下。
如何理解公式?在不考虑 bias的情况下,我们先计算输出feature map中的一个pixel的计算量,然后乘以feature map的规模大小即可,所以主要分析下面FLOPs中的括号部分:
可以看成两个部分,第一项是乘法运算,第二项是加法运算,因为n个数相加,要加n-1次。所以不考虑 bias,会有一个-1,如果考虑bias,刚刚好中和掉了。✖️️2是因为有$C_{int}k^2$次乘法和$C_{int}k^2$次加法??
深度可分离卷积
深度可分离卷积可分为两个部分,第一部分是分通道卷积(深度卷积),另一部分是1*1卷积,两部分相加即可!
Parameters:(不考虑bias)
- 深度卷积:$k^2*C_{int}$
- 1*1卷积:$(11C_{int})*C_{out}$
FLOPs:(考虑bias)
- 深度卷积:$(2k^2 )C_{int}H_{out}W_{out}$
- 1*1卷积:$2C_{int}C_{out}H_{out}W_{out}$
池化层
全局池化:针对输入所有值进行一次池化操作,不论是max、sum还是avg,都可以简单地看做是只需要对每个值算一次。
Parameters:池化层没有可学习的参数,故参数量为0;
FLOPs:$H_{int}W_{int}C_{int}$
一般池化(注意池化层的:$C_{out} = C_{int}$)
- Parameters:池化层没有可学习的参数,故参数量为0;-
- FLOPs:$k^2H_{out}W_{out}*C_{out}$
全连接层
Parameters:
- 考虑bias:$(I+1)*O$
- 不考虑bias:$I*O$
FLOPs:
- 考虑bias:$(2I)O$
- 不考虑bias:$(2I-1)O$
分析同理,括号内是一个输出神经元的计算量,拓展到O个输出神经元。
如果该全连接层的输入是卷积层的输出,需要先将输出展开成一列向量:
例子: $H W D$ 输出到 O,其中参数(包括bias):$(H W D+1) * O$
激活层
- Sigmoid:根据sigmoid的公式可以知道,每个输入都需要经历4次运算,因此计算量是$HWC*4$(参数含义同ReLU)
- Relu:Relu一般都是跟在卷积层的后面,这里假设卷积层的输出为$HWC$,因为ReLU函数的计算只涉及到一个判断,因此计算量就是$HWC$
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 sevenboy!