Loss in Deep Learning

监督学习主要分为两类

  • 回归问题：目标输出变量是连续结果，如预测西瓜的含糖率（0.00~1.00）

  • 分类问题：目标输出变量是离散结果，如判断一个西瓜是好瓜还是坏瓜，那么目标变量只能是1（好瓜）,0（坏瓜）

    • 二分类问题：只有两个类别
    • 多分类问题：多个类别。

损失函数严格上可分为两类：分类损失和回归损失，其中分类损失根据类别数量又可分为二分类损失和多分类损失。在使用的时候需要注意的是：回归函数预测数量，分类函数预测标签。

回归损失函数

平均绝对误差损失(MAE)

平均绝对误差 Mean Absolute Error(MAE) 是常用的损失函数，也称为 L1 Loss，其基本公式为：

简单说就是预测值和标签值差值的绝对值平均值，其可视化图如下图，MAE损失的最小值为0（当预测值等于真实值），最大值为无穷大，可以看出随着预测值与真实值绝对误差 $\left | y_{i} - \hat{y}_i \right |$ 的增加，MAE损失呈线性增长。

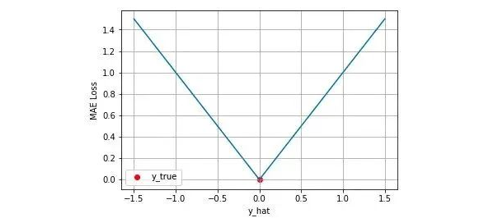
均方差损失(MSE)

均方差 Mean Squared Error (MSE) 损失是机器学习、深度学习回归任务中最常用的一种损失函数，也称为 L2 Loss。其基本形式如下：

损失函数的最小值为 0（当预测等于真实值时），最大值为无穷大。下图是对于真实值 ，不同的预测值 [-1.5, 1.5] 的均方差损失的变化图。横轴是不同的预测值，纵轴是均方差损失，可以看到随着预测与真实值绝对误差 $\left | y_{i} - \hat{y}_i \right |$ 的增加，均方差损失呈二次方地增长。

/>

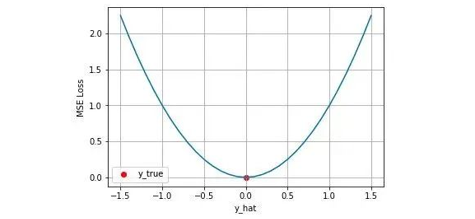MAE和MSE的区别

MAE 和 MSE 作为损失函数的主要区别是：MSE 损失相比 MAE 通常可以更快地收敛，但 MAE 损失对于 outlier 更加健壮，即更加不易受到 outlier 影响。

MSE 通常比 MAE 可以更快地收敛。当使用梯度下降算法时，MSE 损失的梯度为 $-\hat{y}_i$ ，而 MAE 损失的梯度为 $\mp 1$ ，即 MSE 的梯度的 scale 会随误差大小变化，而 MAE 的梯度的 scale 则一直保持为 1，即便在绝对误差很小的时候 MAE 的梯度 scale 也同样为 1，这实际上是非常不利于模型的训练的。当然你可以通过在训练过程中动态调整学习率缓解这个问题，但是总的来说，损失函数梯度之间的差异导致了 MSE 在大部分时候比 MAE 收敛地更快。这个也是 MSE 更为流行的原因.

MAE 对于 outlier 更加 robust，MAE 和 MSE 损失函数可视化中，由于MAE 损失与绝对误差之间是线性关系，MSE 损失与误差是平方关系，当误差非常大的时候，MSE 损失会远远大于 MAE 损失。因此当数据中出现一个误差非常大的 outlier 时，MSE 会产生一个非常大的损失，对模型的训练会产生较大的影响。

Huber Loss

MSE损失收敛快但是容易收到 outlier 的影响，MAE对 outlier 更加健壮但是收敛满，Huber Loss则是一种将 MSE 和 MAE结合起来，取二者优点的损失函数，也称为 Smooth Absolute Error Loss，其原理就是在误差接近0的时候使用 MSE，误差较大时使用 MAE，公式为：

其中 $\delta$ 是 Huber Loss 的一个超参数， $\delta$ 的值是在 MSE 和 MAE 两个损失连接的位置，上述等式第一项是 MSE 部分。第二项是 MAE 部分，在MAE部分公式为 $\delta\left|y_{i}-\hat{y}_{i}\right|-\frac{1}{2} \delta^{2}$ 是为了保证误差 $\left | y_{i} - \hat{y}_i \right | = \mp \delta$ 时，MAE和MSE的取值是一致的，进而保证 Huber Loss损失连续可导。下图是 $\delta = 1.0$ 时的 Huber Loss，可以看到在区间 $[-\delta,\delta]$ 就是MSE损失，在区间 $(-\infty,\delta)$ 和 $(\delta, +\infty)$ 就是MAE损失：

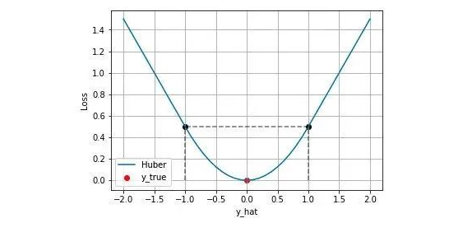
Huber Loss 结合了 MSE 和 MAE 损失，在误差接近 0 时使用 MSE，使损失函数可导并且梯度更加稳定；在误差较大时使用 MAE 可以降低 outlier 的影响，使训练对 outlier 更加健壮。缺点是需要额外地设置一个 $\delta$ 超参数。

分类损失

交叉熵损失(CrossEntropy Loss)

交叉熵损失函数是分类中最常用的损失函数，交叉熵是用来度量两个概率分布的差异性的，用来衡量模型学习到的分布和真实分布的差异。

在二分类中，通常使用 Sigmoid 函数将模型的输出压缩到 【0，1】区间内，$\hat{y}_i \in (0,1)$, 用来代表给定输入 $x_i$ ，模型判断为为正类的概率。因此也得到负类的概率，

二分类交叉熵损失（binary entropy loss）的一般形式：P为正类概率，y为标签。

交叉熵公式的原理：

  • 信息量，信息量表示一条信息消除不确定性的程度，信息量的大小和事件发生的概率成反比

  • 信息熵，信息熵则是在结果出来之前对可能产生的信息量的期望，期望可以理解为所有可能结果的概率乘以该对应的结果。

    信息熵是用来衡量事物不确定性的。信息熵越大（信息量越大，P越小），事物越具不确定性，事物越复杂。

  • 相对熵（KL散度），相对熵又称互熵 设 P(x) 和 Q(x) 是取值的两个概率分布，相对熵用来表示两个概率分布的差异，当两个随机分布相同时，他们的相对熵为0，当两个随机分布的差别增大时，他们的相对熵也会增大：

    • KL散度不是一个对称量，$D_{K L}(P | Q) \neq D_{K L}(Q | P)$。
    • KL散度的值始终大于>=0,当且仅当 $P(X)=Q(x)$ 等号成立。

交叉熵， KL散度换种写法：

交叉熵 $H(P,Q)$ 即等于 信息熵+KL散度：

把 P 看作随机变量的真实分布的话，KL散度左半部分 $ -H(P(X))$ 的信息熵其实是一个固定值，KL散度的大小变化其实是由右半部分交叉熵来决定的，因为右半部分含有近似分布 Q，我们可以把它看作网络或模型的实时输出，把KL散度或者交叉熵看做真实标签与网络预测结果的差异，所以神经网络的目的就是通过训练使近似分布逼近真实分布。从理论上讲，优化KL散度与优化交叉熵的效果应该是一样的。所以我认为，在深度学习中选择优化交叉熵而非KL散度的原因可能是为了减少一些计算量，交叉熵毕竟比KL散度少一项。

多分类交叉熵损失，多分类和二分类类似，二分类的标签为1和0，而多分类可以用one-hot编码来表示，公式为：

其中，$y_{i,k}$ 表示第 i 个样本的真实标签为 k，共有 K 个标签值 N 个样本，$p_{i,k}$ 表示第 i 个样本预测为第 k 个标签值得概率，通过对该损失函数得拟合，也在一定程度上增大了类间距离，在 torch中，torch.nn.functional.cross_entropy 实现了将输出整合到【0，1】概率区间，不需要 softmax 操作。

Weight Loss

交叉熵Loss可以用在大多数语义分割场景中，但它有一个明显的缺点，那就是对于只用分割前景和背景的时候，当前景像素的数量远远小于背景像素的数量时，即 y=0 的数量远大于 y=1 的数量，损失函数中 y=0 的成分就会占据主导，使得模型严重偏向背景，导致效果不好。

由于交叉熵损失会分别评估每个像素的类别预测，然后对所有像素的损失进行平均，因此我们实质上是在对图像中的每个像素进行平等地学习。如果多个类在图像中的分布不均衡，那么这可能导致训练过程由像素数量多的类所主导，即模型会主要学习数量多的类别样本的特征，并且学习出来的模型会更偏向将像素预测为该类别。

FCN论文和U-Net论文中针对这个问题，对输出概率分布向量中的每个值进行加权，即希望模型更加关注数量较少的样本，以缓解图像中存在的类别不均衡问题。

比如对于二分类，正负样本比例为1: 99，此时模型将所有样本都预测为负样本，那么准确率仍有99%这么高，但其实该模型没有任何使用价值。

为了平衡这个差距，就对正样本和负样本的损失赋予不同的权重，带权重的二分类损失函数公式如下：

要减少假阴性样本的数量，可以增大 pos_weight；要减少假阳性样本的数量，可以减小 pos_weight。

带权重的交叉熵Loss，公式为：

可以看到只是在交叉熵Loss的基础上为每一个类别添加了一个权重参数，其中 $w_c$ 的计算公式为： $w_c = \frac{N-N_c}{N}$ 其中 N 表示总的像素个数，而 $N_c$ 表示 GT 类别为 c 的像素个数。这样相比于原始的交叉熵Loss，在样本数量不均衡的情况下可以获得更好的效果。

Focal Loss

重点：需要解决不同类别的像素数量不均衡问题，但有时还需要将像素分为难学习和容易学习这两种样本。

容易学习的样本模型可以很轻松地将其预测正确，模型只要将大量容易学习的样本分类正确，loss就可以减小很多，从而导致模型不怎么顾及难学习的样本，所以我们要想办法让模型更加关注难学习的样本。

何凯明团队在RetinaNet论文中引入了Focal Loss来解决难易样本数量不平衡，我们来回顾一下。 我们在计算分类的时候常用的损失——二分类交叉熵的公式如下：

为了解决正负样本数量不平衡的问题，我们经常在二元交叉熵损失前面加一个参数 $\alpha$，即：

虽然参数 $\alpha$ 平衡了正负样本的数量，上式针对不同类别的像素数量不均衡提出了改进方法。但实际上，有时候候选目标都是易分样本。这些样本的损失很低，但是由于数量极不平衡，易分样本的数量相对来讲太多，最终主导了总的损失。

因此，这篇论文认为易分样本（即，置信度高的样本）对模型的提升效果非常小，模型应该主要关注与那些难分样本 。所以Focal Loss横空出世了。一个简单的想法就是只要我们将高置信度样本的损失降低一些就好了吧？ 也即是下面的公式：

其中的 $\gamma$ 通常设置为2。

举个例子，预测一个正样本，如果预测结果为0.95，这是一个容易学习的样本，有 $(1−0.95)^2=0.0025$ ，损失直接减少为原来的1/400。

而如果预测结果为0.5，这是一个难学习的样本，有 $(1−0.5)^2=0.25$ ，损失减小为原来的1/4，虽然也在减小，但是相对来说，减小的程度小得多。

所以通过这种修改，就可以使模型更加专注于学习难学习的样本。

而将这个修改和对正负样本不均衡的修改合并在一起，就是大名鼎鼎的 focal loss：带两个超参数：$\alpha$ 和 $\gamma$

Focal Loss代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class FocalLoss(nn.Module):
    def __init__(self, gamma=0, alpha=None, size_average=True):
        super(FocalLoss, self).__init__()
        self.gamma = gamma
        self.alpha = alpha
        if isinstance(alpha,(float,int,long)): self.alpha = torch.Tensor([alpha,1-alpha])
        if isinstance(alpha,list): self.alpha = torch.Tensor(alpha)
        self.size_average = size_average

    def forward(self, input, target):
        if input.dim()>2:
            input = input.view(input.size(0),input.size(1),-1)  # N,C,H,W => N,C,H*W
            input = input.transpose(1,2)    # N,C,H*W => N,H*W,C
            input = input.contiguous().view(-1,input.size(2))   # N,H*W,C => N*H*W,C
        target = target.view(-1,1)

        logpt = F.log_softmax(input)
        logpt = logpt.gather(1,target)
        logpt = logpt.view(-1)
        pt = Variable(logpt.data.exp())

        if self.alpha is not None:
            if self.alpha.type()!=input.data.type():
                self.alpha = self.alpha.type_as(input.data)
            at = self.alpha.gather(0,target.data.view(-1))
            logpt = logpt * Variable(at)

        loss = -1 * (1-pt)**self.gamma * logpt
        if self.size_average: return loss.mean()
        else: return loss.sum()