Vision_Transformer相关总结

Transformer的小总结

$$Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$$

计算过程：$Q,K,V \in R^{B \times H \times W \times C}$ ==> 多头注意力$Q,K,V \in R^{B \times \times H \times W \times numHead \times C/numHead} ==>Q,k,V \in R^{B \times numHead \times HW \times C/numHead }$ ==> 注意力矩阵 $S = QK^T \in R^{B \times numHead \times HW \times HW}$==>提取value $SV \in R^{B \times numHead \times HW \times C/numhead} ==> R^{B \times HW \times C}$

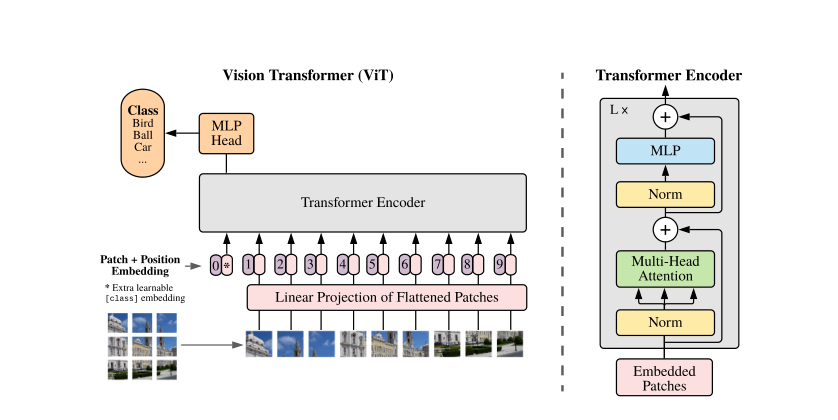
Transformer简要介绍

• Transfomer 是一种基于注意力机制的神经网络模型。Transformer模型由编码器和解码器两部分组成，其中编码器用于将输入序列编码成一个高维向量表示，解码器用于将这个向量表示解码成目标序列。Transformer模型最核心的部分是自注意力机制，它能够让模型在不同位置之间进行信息传递和交互，从而更好地学习输入序列中的信息。

Transformer的输入是什么

• Trransformer的输入是词向量与位置向量之和，词向量可以通过预训练的词向量模型或在模型内部学习得到。位置向量可以通过固定位置编码公式获得或者在模型内容不学习得到。

• Vision Transformer：首先将图像进行patch化策略，把每一个patch视为向量，所有向量并在一起就形成一系列的patch序列，然后再加上位置编码作为Transformer的输入。

  self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size) patch_size:也就是下采样的倍数，一般为4、16

固定编码和可学习编码的优缺点

• 固定位置编码优点是可以根据公式快速获得句子的位置信息，无需在训练中继续学习；其缺点是不能处理变化的序列（例如：我是大帅哥，大帅哥是我）。
• 可学习位置编码优点是可以通过训练时动态理解句子的位置信息；缺点是需要大量的数据才能获取比较全的位置信息。

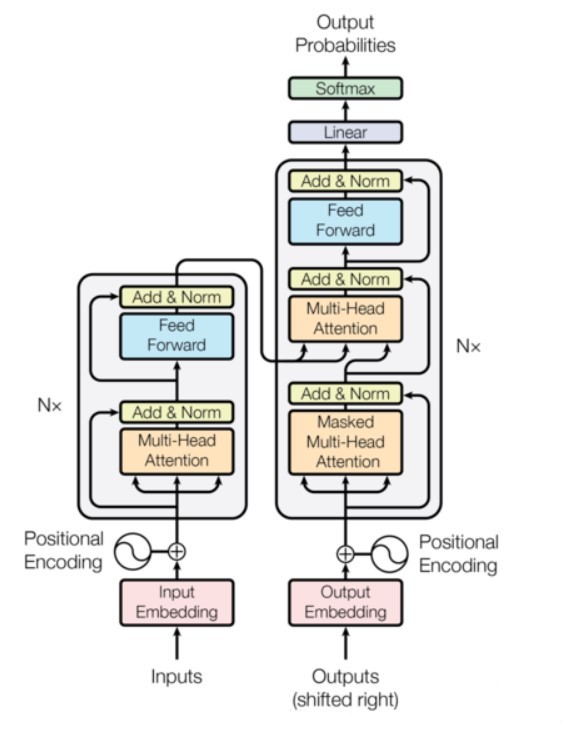
Transformer的Encoder模块

• Transformer的Encoder模块是由多个相同的层堆叠而成的，每一层由两个子层组成，分别是多头注意力机制（Multi-Head Attention）和前馈神经网络（Feed-Forward Neural Network）。在多头注意力机制中，输入序列会经过三个线性变换，分别是Q、K、V，然后进行多头注意力计算，得到每个位置对其他位置的注意力权重，再将输入序列加权求和得到多头注意力的输出。在前馈神经网络中，多头注意力的输出经过两个全连接层和ReLU激活函数的变换，得到每个位置的特征表示。接下来，这两个子层会进行残差连接（Residual Connection）和层归一化（Layer Normalization）操作，使得模型更容易训练，也能更好地捕捉输入序列之间的相关性。
• 残差结构以及意义：encoder和decoder的self-attention层和ffn层都有残差连接。反向传播的时候不会造成梯度消失。

为什么transformer块使用LayerNorm而不是BatchNorm？

• Layer Normalization是一种能够应对不同序列长度的归一化方法，它对每个样本的特征进行归一化。Batch Normalization是一种在深度神经网络中广泛使用的归一化方法，通过对每个小批量的输入进行归一化，从而使得网络的训练更加稳定，并加速收敛速度。但是，在自然语言处理任务中，输入的序列长度通常是不同的，因此很难将不同长度的序列组成一个小批量进行归一化。
• Batchnorm为批归一化，对相同批次中所有样本的同一位置特征做归一化，而layernorm是对某个样本的所有位置特征做归一化。BN归一化会抹去同一样本所有位置特征的原有大小关系，LN会保留这种大小关系。

Transformer输入只能相加吗？

• 在Transformer模型中，输入的两个部分是词向量和位置编码，它们是分别生成的，然后进行相加得到最终的输入表示。因此，在Transformer模型中，输入确实只能相加，即词向量和位置编码不能进行其他的运算，如乘法、除法等。这是因为词向量和位置编码的维度是相同的，都是模型的隐藏层维度，而它们的作用是不同的，词向量用于表示单词的语义信息，位置编码用于表示单词在句子中的位置信息。因此，将它们相加可以将这两种信息融合到一起，从而为模型提供更加丰富的输入信息。如果进行其他的运算，如乘法、除法等，可能会破坏词向量和位置编码的信息，影响模型的性能。因此，在Transformer模型中，输入只能相加，不能进行其他的运算。

Transformer为何使用多头注意力机制？

• 提高模型的表达能力，多头注意力机制可以让模型在不同的注意力空间下学习到不同的特征，从而能够更好地表达输入序列的信息。如果只使用一个注意力头，那么模型可能会在学习特定的特征时出现瓶颈，导致模型的表达能力受限。
• Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.
• 举例说明不一样的特征表达字空间。一张图中在颜色方面更加关注鲜艳亮丽的文字，而在字体方面会去注意大的、粗体的文字。

Transformer为什么Q和K使用不同的权重矩阵生成，为何不能使用同一个值进行自身的点乘？

• 使用 Q；K；V 不相同可以保证在不同空间进行投影，增强了表达能力，提高了泛化能力。
• 在Transformer中，Q和K使用不同的权重矩阵生成是为了让模型在学习不同的特征时更加灵活。Q和K的区别在于它们所代表的信息不同，Q代表查询信息，K代表键信息，它们的作用不同，因此使用不同的权重矩阵可以让模型在不同的注意力空间下学习到更加丰富的特征，并提高模型的表现能力。
• 如果使用同一个权重矩阵进行自身的点乘操作，可能会使模型在学习特定的特征时出现瓶颈，导致模型表达能力受限，从而影响模型的性能。
• 为了打破对称性，但是如果不用Q，直接拿K和K点乘的话，你会发现attention score 矩阵是一个对称矩阵。因为是同样一个矩阵，都投影到了同样一个空间，所以泛化能力很差。

Transformer计算attention的时候为何选择点乘而不是加法？

• K和Q的点乘是为了得到一个attention score 矩阵，用来对V进行提纯。K和Q使用了不同的W_k, W_Q来计算，可以理解为是在不同空间上的投影。正因为有了这种不同空间的投影，增加了表达能力，这样计算得到的attention score矩阵的泛化能力更高。

• 在Transformer中，采用点乘（dot-product）作为注意力机制的计算方式，是因为点乘计算的方式是一种更加有效的方法，可以更好地捕捉输入序列中的相关性。与加法相比，点乘可以使模型在计算注意力时更加精确，同时也具有更好的计算效率。

在计算attention时，为什么进行softmax之前需进行scaled（为什么除以dk的平方根）?

• 在计算self-attention时，需要进行softmax操作，以计算每个输入序列位置对其他位置的注意力权重。为了避免softmax函数的指数计算导致数值溢出或下溢，Transformer模型中使用了scaled dot-product attention，即在softmax之前对向量点乘结果进行了缩放操作，用于控制点乘结果的大小。
  具体来说，该缩放操作是将点乘结果除以一个值，这个值是输入向量的维度的平方根，即dk的平方根，其中dk表示每个向量的维度。这个缩放因子的作用是：当输入向量的维度增加时，点乘结果的大小也会增加，导致softmax函数的指数计算变得困难，缩放因子能够使点乘结果的大小保持在一个合适的范围内，从而提高计算的稳定性。

大概讲一下Transformer的Decoder模块？

• Transformer模型的Decoder模块是用于将Encoder模块的输出映射到目标序列的一组连续表示的核心部分。该模块由多个Decoder层组成，每个Decoder层包括了以下几个部分：
  1. 自注意力层：与Encoder中的自注意力层类似，Decoder中的自注意力层也是将输入序列中每个位置的表示向量作为查询向量(Q)、键向量(K)和值向量(V)，通过多头注意力计算得到每个位置的上下文向量。但是多了一个Mask的过程，让输入序列只看到过去的信息，不能让他看到未来的信息。具体来说，在attention score矩阵中添加mask矩阵来屏蔽不可见的信息，对padding做mask操作就是在padding位置设为负无穷(一般来说-1000就可以)，再对attention score进行相加即可。
  2. 编码器-解码器注意力层(cross-attention)：该层用于将Encoder模块的输出与Decoder中上一层的输出结合起来，以便更好地理解输入和输出之间的关系。具体来说，该层将Encoder模块的输出作为键向量(K) 和值向量(V) ，将Decoder中上一层的输出作为查询向量(Q)，通过多头注意力机制计算得到每个位置的上下文向量。
  3. 前馈神经网络层：该层对经过自注意力层和编码器-解码器注意力层编码的信息进行非线性变换，以提高模型的表达能力。
  4. 残差连接层和层归一化层：这两个层与Encoder模块中的残差连接层和层归一化层类似，用于保证模型的稳定性和加速训练。在每个Decoder层之间，都进行了层归一化处理。
     Decoder模块的最后一层输出的表示向量经过一个线性变换和softmax函数，得到每个位置上每个单词的概率分布。然后可以根据分布进行单词的选择和预测。

Decoder阶段的多头自注意力和encoder的多头自注意力有什么区别？

• 在Transformer模型中，Encoder和Decoder都包含多头自注意力机制。虽然它们的原理类似，但是在具体实现中，它们之间存在一些区别。下面分别介绍Decoder阶段的多头自注意力和Encoder的多头自注意力的区别：

  1.查询向量不同：在Encoder的多头自注意力中，每个词向量都被用作查询、键和值，即Q=K=V，而在Decoder的多头自注意力中，查询向量(Q) 是上一个Decoder层的输出，而键(K) 和值向量(V) 是Encoder模型的输出。

  2.掩码：在Decoder的多头自注意力中，需要使用掩码来防止当前时间步的解码器看到未来时间步的信息。具体来说，将未来时间步的位置的注意力权重设置为0，这样在计算当前时间步的注意力分数时，就不会考虑未来时间步的信息。

  3.添加编码：在Decoder的多头自注意力中，需要将编码器的输出添加到查询向量和键向量中，以便解码器能够了解输入序列的信息。

  4.位置编码：在Decoder的多头自注意力中，位置编码的计算方式与Encoder中的位置编码不同。Encoder中的位置编码是为了表示输入序列中单词的位置关系，而Decoder中的位置编码是为了表示输出序列中单词的位置关系。

Transformer的并行化提现在哪个地方？Decoder端可以做并行化吗？

• 1. 多头注意力机制：多头注意力机制将输入序列分成多个子序列，并同时计算每个子序列的注意力表示，从而实现了多头并行计算。这种并行计算方式可以有效地加速模型的训练和推理过程。

  2. Encoder端的并行化：在Encoder端，Transformer模型将输入序列分成多个子序列，并分别在不同的计算设备上进行计算。这种并行计算方式可以显著提高模型训练的速度。而在Decoder端，由于每个时间步的计算需要依赖上一个时间步的输出，因此无法进行完全的并行化。但是，可以通过一定的技巧来提高Decoder的并行化效率，例如：

  3. 延迟解码：在训练时，可以将目标序列分成多个子序列，并在不同的计算设备上同时进行解码。但是，在推理时，由于无法知道整个目标序列，因此需要使用延迟解码的方式，即在每个时间步上进行解码，并将上一个时间步的输出作为当前时间步的输入。

  4. Beam Search并行化：在推理时，可以使用Beam Search算法来生成目标序列，并通过将不同的Beam分配到不同的计算设备上来实现推理的并行化。
  因此，虽然Decoder端无法像Encoder端那样进行完全的并行化，但是可以通过一定的技巧来提高其并行化效率。

简单描述一下Transformer中的前馈神经网络？使用了什么激活函数？相关优缺点？

• Transformer模型中的前馈神经网络（Feed-Forward Neural Network，简称FFN）是在每个Encoder和Decoder层的自注意力层和编码器-解码器注意力层之间添加的一层全连接的前馈神经网络。它的输入是自注意力层或编码器-解码器注意力层的输出，输出是一个新的表示向量，其中包含了更高层次的语义信息。
  在Transformer模型中，FFN使用了两层全连接的结构，两层之间使用了ReLU激活函数。具体来说，在每个FFN层中，输入的表示向量首先通过一个全连接层进行线性变换，然后再通过一个ReLU激活函数进行非线性变换，最后再通过另一个全连接层进行线性变换得到输出。
  FFN的优点是可以通过多层的非线性变换，提取输入的更高层次的语义特征，从而提高模型的表达能力。另外，由于FFN的计算是独立进行的，因此可以通过并行化来加速模型的训练和推理过程。
  但是，FFN也存在一些缺点。首先，由于FFN只考虑了每个位置的局部信息，因此无法处理序列中的长距离依赖关系。其次，由于FFN的计算复杂度较高，因此容易成为模型的瓶颈。最后，由于FFN没有考虑序列中的位置信息，因此可能会存在位置信息的混淆问题。
  为了解决这些问题，一些变种的Transformer模型，如XLNet和Relative Positional Encoding等，引入了新的机制，以提高模型的性能和稳定性。

分析计算复杂度

• Vision Transformer 中计算复杂度是平方次幂级别的，具有高计算量和内存消耗；这也在最近大量论文针对解决的问题，降低2次幂的复杂度问题。

• 分析Vision Transformer的计算复杂度：

  • Multi-head Attention：输入query, key, value; 其中query, key首先通过矩阵相乘得到一个attention矩阵，然后 attention 矩阵再通过和value进行矩阵相乘得到了加了attention信息的feature。我们知道query，key，value来自同一个feature，但是需要通过三个不一样的全连接层映射到不一样的投影空间。假设输入的 feature 的特征维度是：$N \times D \times H \times W$, 分别通过三个不一样的全连接层 $D \times D$， 此处他们三个的权值是不共享的，所以：

    • 参数量：$3 \times D \times D$ ；计算量： $3 \times HW \times D \times D$ ；其中3就是三个不一样的全连接层分别得到q，k，v。

    接下来是multi-head的过程，multi-head的原理是把通道维度D分为多个head，每个head学习不同方面的attention信息，同时参数量和计算量也不会额外增加。只包含计算两次矩阵相乘的结果：

    • query@key and attention_map@value：$2 \times (HW)^2 \times D$;

    最后再接一个全连接层：

    • 参数量：$D \times D$ ；计算量： $ HW \times D \times D$ ；

    总结：

    参数量：$4 \times D \times D$ ；计算量： $4 \times HW \times D^2 + 2(HW)^2 \times D$ ；2次幂指的是$(HW)^2$

  • FFN过程：经过两个全连接层：计算量为 $2 \times HW \times D \times D_{hiddn}$

• 减少计算量的主要方面：

  • 1、Token 通道修剪：就是修剪一开始线性生成q，k，v的 feature 的通道D，意味着减少了全连接层的计算量
  • 2、Token 数量的修剪：就是减少 HW（N）的数量，这会直接影响到2次幂的关键，也是最常见的减少计算量的方式
  • 3、Attention 通道的修剪：就是减少计算attention时的通道数目。

VIT和CNN的对比分析

卷积（Convolution）来对输入的图像进行特征提取。卷积的计算范围是在像素点的空间邻域内进行的，因此可以利用输入图像的空间信息；此外，由于卷积具有局部连接、权重共享等特性，卷积核参数的数目也远小于全连接层。

1. 局部连接：全连接层是一种稠密连接方式，而卷积层却只使用卷积核对局部进行处理，这种处理方式其实也刚好对应了图像的特点。在视觉识别中，关键性的图像特征、边缘、角点等只占据了整张图像的一小部分，相隔很远的像素之间存在联系和影响的可能性是很低的，而局部像素具有很强的相关性。
2. 共享参数：如果借鉴全连接层的话，对于1000×1000大小的彩色图像，一层全连接层便对应于三百万数量级维的特征，即会导致庞大的参数量，不仅计算繁重，还会导致过拟合。而卷积层中，卷积核会与局部图像相互作用，是一种稀疏连接，大大减少了网络的参数量。另外从直观上理解，依靠卷积核的滑动去提取图像中不同位置的相同模式也刚好符合图像的特点，不同的卷积核提取不同的特征，组合起来后便可以提取到高级特征用于最后的识别检测了。

• CNN的归纳偏置(Inductive Bias)主要有两种：局部感知性(locality )；平移不变性( translation equivariance) ==>需要较少的数据去学好一个模型
• VIT中的自注意力机制层是全局的，比CNN结构少了一定的平移不变性和局部感知性，在数据量较少的情况下，效果可能不如CNN模型，但是在大规模数据集上预训练过后，再进行迁移学习，可以在特定任务上达到SOTA性能。

Transformer与LSTM的对比

• 是对RNN存在的梯度消失、梯度爆炸问题的一种优化模型。

• LSTM引入三个控制门（输入门，输出门，遗忘门），拥有了长期记忆，更好的解决了RNN的梯度消失和梯度爆炸问题。

• LSTM的三个门的作用：输入门决定何时让输入进入细胞单元；遗忘门决定何时应该记住前一时刻的信息；输出门决定何时让记忆流入下一时刻。

• LSTM包含了两种激活函数，sigmoid 用在了各种门限上，产生0~1之间的值。tanh 用在了状态和输出上，是对数据的处理。

• LSTM是怎么解决梯度消失的问题的？

  传统的神经网络层数一多，就会有梯度消逝和爆炸的现象，因为导数的链式法则导致了连乘的形式。造成梯度指数级的消失，lstm使用CEC(constant error carousel)机制，使得远处的梯度传到近处没有改变、但这样又会造成输入输出权重矛盾，所以又使用了门限单元来解决。

  因为lstm有两个通道可以保持记忆：短期记忆h，保持非线性操作；长期记忆C，保持线性操作。因为线性操作是比较稳定的，所以C的变化相对稳定，保持了长期记忆。而对有用信息的长期记忆是通过训练获得的，也就是说在内部的几个权重矩阵中。

  LSTM总可以通过选择合适的参数，再不发生梯度爆炸的情况下，找到合理的梯度方向来更新参数，而且这个方向可以充分考虑远距离的隐藏层信息的传播影响。

• Transformer相对于LSTM的优势

  • 并行计算：RNN 和LSTM 需要顺序处理序列数据，有时许的概念，因此很难进行并行计算。而 Transformer 的 自注意力机制允许同时处理整序列，从而可以充分利用 GPU 的并行计算能力，大大提高模型训练和推理的速度。
  • 可解释性：Transformer 中的自注章力机制为每个位置的输出都分配了一个权重，这些权重表明了输入序列中不同位置对于输出的贡献。这使得 Transformer 更具可解释性，可以直观地观察模型在处理序列数据时关注的区域。
  • 模型容量：Transformer 可以很容易地堆叠多层，从而增加模型容量，多层 Transformer 结构可以让模型学习更复杂和抽象的表示。

  尽管 Transformer 在许多方面具有优势，但它也有一些局限，如需要大量的计算资源和内存，以及可能产生较高的计算复杂度，