最长递增子序列
动态规划—两道有趣的题目
one:eetcode 300最长递增子序列
https://leetcode-cn.com/problems/longest-increasing-subsequence/submissions/
1、题目大意

2、分析
看到题目,判断某一个数组的最长递增子序列,注意并不是连续的。
3、方法1:完全递归
现在假设下标 i 结尾的数组的最唱递增子序列为 max,
若nums[i+1]>nums[i] ; 则下标 i+1 结尾的数组的最唱递增子序列为 max+1,否则为 max
所以这个题目是可以拆解子问题的,有子问题最后堆砌到最终答案
设 函数 fun(n,nums) : 表示在数组nums下,以n作为下标的最大递增序列
得到递归方程 :fun(n,nums) = fun(j,nums)+1 其中 0<=j<i 并且 dp[j]<dp[i] j为【0,i】里面的任意值,需要遍历
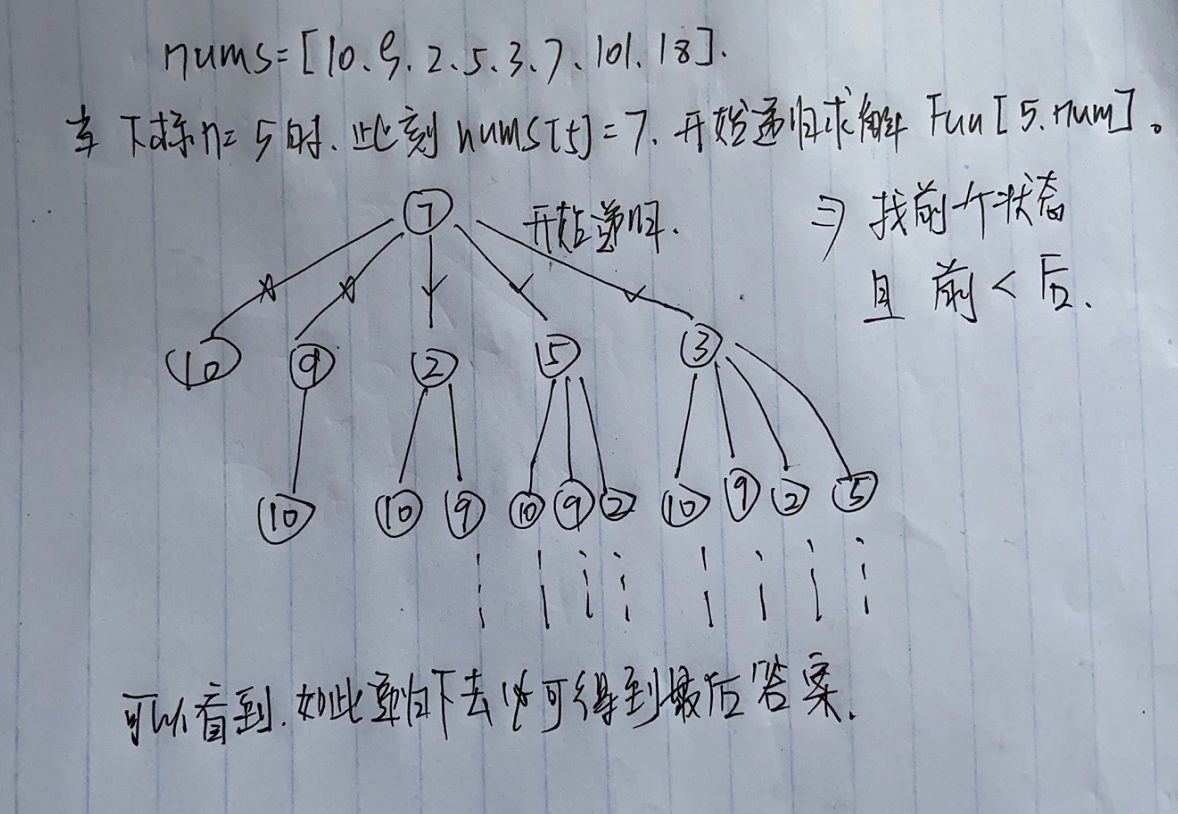
拿下图为递归树(简约哈)
代码:
1 | int main(){ |
当然,这样递归的结果就是,提交超时,hhhhhhh。但是没关系,思路对了,下面进行优化。
4、方法2:记忆化加递归
在方法一的基础上,我们可以记录一个记忆化的数组,在递归刚刚开始的时候去判断这个数组是否有值,有的话直接递归返回了,若没有,则进行递归
再拿上一张图片来看,比如递归到数字 2 的时候,我们记录好递归到数字 2 的记忆数组值,当下次在别的树枝上需要递归数字 2 的时候,便可以直接取了,而不用继续遍历了,效率会高很多

代码
1 | int main(){ |
这次提交,是可以通过的,足见时间效率上提高了可不少。
5、方法3:动态规划
根据上述两个方法的分析的,可以很容易得到动态规划的状态转移方程
dp[i] : 表示以 i 为下标结尾的数组的最长递增字符串
状态转移方程
1
dp[i] = max(dp[j]+1) 其中 0<=j<i 并且 dp[j]<dp[i] j为[0,i]里面的任意值,需要遍历
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27int main(){
int nums[] = {10,9,2,5,3,7,101,18};
int numSize = sizeof(nums) / sizeof(nums[0]);
printf("%d",lengthOfLI(nums,numSize));
}
int lengthOfLIS(int* nums, int numsSize){
//最后的最大值
int ansMax = 1;
//1、建立dp数组
int dp[numsSize];
memset(dp, 0, sizeof(int) * numsSize);
//2、递归遍历,封装dp数组
for (int i = 0; i < numsSize;i++)
{
//记录遍历j属于【0,i】里面的最大值。初始值为1,表示本身
int max = 1;
for (int j = 0; j < i;j++)
{
if(nums[j]<nums[i]) max = fmax(max, dp[j] + 1);
}
//给dp赋值
dp[i] = max;
//每次比较,取最大
ansMax = dp[i] > ansMax ? dp[i] : ansMax;
}
return ansMax;
}这个是比较常规的方法了:时间复杂度是 O(N*N)
6、方法4:贪心+二分查找
- 考虑一个简单的贪心,如果我们要使上升子序列尽可能的长,则我们需要让序列上升得尽可能慢,因此我们希望每次在上升子序列最后加上的那个数尽可能的小。
- 基于上面的贪心思路,我们维护一个数组 dp[i] ,表示长度为 i 的最长上升子序列的末尾元素的最小值,用 len 记录目前最长上升子序列的长度,起始时len =1,d[1]=nums[0]。
由定义知dp数组必然是一个递增数组, 对原数组nums进行迭代, 依次判断每个数num将其插入dp数组相应的位置:
- num > dp[len], 表示num比所有已知递增序列的尾数都大, 将num添加入dp 数组尾部, 并将最长递增序列长度len加1
- dp[i-1] < num <= dp[i], 只更新相应的dp[i]=num
以 nums=[4,10,3,8,9]:
1)第一步插入4,则 dp=[4]
2) 第二步插入10,则dp=[4,10]
3) 第三步插入3,原数组4的位置更新为3 则dp=[4,10]==》dp=[3,10]
4) 第四步插入8,原数组10的位置更新为8 则dp=[4,10]==》dp=[3,8]
5) 第五步插入9,则dp=[3,8,9]
所以最后的答案为 len(dp) = 3;
代码:
1 | int main(){ |
two :354 俄罗斯套娃
https://leetcode-cn.com/problems/russian-doll-envelopes/
1、题目大意
2、分析
根据题目的要求,如果我们选择了 k 个信封,它们的
宽度依次为 w0, w1, ···, w k-1 高度依次为 h0, h1,···, h k-1 ,那么需要满足如下了两个条件:
同时控制 w 和 h 两个维度并不是那么容易,因此我们考虑固定一个维度,再在另一个维度上进行选择。例如,我们固定 w 维度,那么我们将数组envelopes 中的所有信封按照 w 升序排序。这样一来,我们只要按照信封在数组中的出现顺序依次进行选取,就一定保证满足:
然而小于等于 ≤ 和小于 <还是有区别的,但我们不妨首先考虑一个简化版本的问题:
如果我们保证所有信封的 w 值互不相同,那么我们可以设计出一种得到答案的方法吗?
在 w 值互不相同的前提下,小于等于≤ 和小于 < 是等价的,那么我们在排序后,就可以完全忽略 w 维度,只需要考虑 h 维度了。此时,我们需要解决的问题即为:
给定一个序列,我们需要找到一个最长的子序列,使得这个子序列中的元素严格单调递增,即上面要求的:
那么这个问题就是经典的「最长严格递增子序列」问题,问题得到解决,
当我们解决了简化版本的问题之后,我们来想一想使用上面的方法解决原问题,会产生什么错误?当 w 值相同时,如果我们不规定 h 值的排序顺序,那么可能会有如下的情况:
排完序的结果为 [(w, h)] = [(1, 1), (1, 2), (1, 3), (1, 4)][(w,h)]=[(1,1),(1,2),(1,3),(1,4)],由于这些信封的 w 值都相同,不存在一个信封可以装下另一个信封,那么我们只能在其中选择 1 个信封。然而如果我们完全忽略 w 维度,剩下的 h 维度为 [1, 2, 3, 4][1,2,3,4],这是一个严格递增的序列,那么我们就可以选择所有的 4 个信封了,这就产生了错误。
因此,我们必须要保证对于每一种 w 值,我们最多只能选择 1 个信封。
我们可以将 h 值作为排序的第二关键字进行降序排序,这样一来,对于每一种 w 值,其对应的信封在排序后的数组中是按照 h 值递减的顺序出现的,那么这些 h 值不可能组成长度超过 1 的严格递增的序列,这就从根本上杜绝了错误的出现。
因此我们就可以得到解决本题需要的方法:
首先我们将所有的信封按照 w 值第一关键字升序、h 值第二关键字降序进行排序;
随后我们就可以忽略 w 维度,求出 h 维度的最长严格递增子序列,其长度即为答案。
- 至此分析完了,归根到底就是最长递增子序列的问题了
3、代码
直接show code no say say
常规动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50int main(){
int* p[4];
int points[4][4] = {{5,4},{6,4},{6,7},{2,3}};
p[0] = &points[0][0];
p[1] = &points[1][0];
p[2] = &points[2][0];
p[3] = &points[3][0];
int envelopesSize = 4;
int envelopesColSize[] = {2,2,2,2};
int ans = maxEnvelopes1(p,envelopesSize,envelopesColSize);
printf("%d", ans);
}
//方法一:普通动态规划
//dp[i]:表示以下标i为结尾的最大增序列 再次遍历取其最大
//状态转移方程 dp[i] = dp[j]+1 其中 j<i 并且排好序的envelopes中envelopes[j][1] <envelopes[i][1]
int maxEnvelopes(int** envelopes, int envelopesSize, int* envelopesColSize){
//1、先排序,首先按照第一列升序排序,若第一列的值相同,则按照第二列的值降序排序
qsort(envelopes, envelopesSize, sizeof(int*), compare);
//2、构建dp数组
int dp[envelopesSize+1];
memset(dp, 0, sizeof(dp[0]) * (envelopesSize + 1));
//3、根据状态转移方程,递推求dp
for (int i = 1; i <= envelopesSize;i++)
{
//遍历【1,i】位置 找符合条件的最大dp[j]+1
int max = 1;
for (int j = 1; j < i;j++)
{
if(envelopes[i-1][1]>envelopes[j-1][1]) max = fmax(max, dp[j] + 1);
}
//赋值给dp
dp[i] = max;
}
//4、取其最大
int ans = 1;
for (int i = 0; i < sizeof(dp) / sizeof(dp[0]); i++)
{
ans = dp[i] > ans ? dp[i] : ans;
}
return ans;
}
//第一个参数升序 第二个参数降序
int compare(const void *a, const void *b){
int* num1 = *(int**)a;
int* num2 = *(int**)b;
if(num1[0]==num2[0]) return num2[1] - num1[1];
else return num1[0] - num2[0];
}基于二分查找的动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54int main(){
int* p[4];
int points[4][4] = {{5,4},{6,4},{6,7},{2,3}};
p[0] = &points[0][0];
p[1] = &points[1][0];
p[2] = &points[2][0];
p[3] = &points[3][0];
int envelopesSize = 4;
int envelopesColSize[] = {2,2,2,2};
int ans = maxEnvelopes1(p,envelopesSize,envelopesColSize);
printf("%d", ans);
}
//方法二:基于二分查找的动态规划
int maxEnvelopes1(int** envelopes, int envelopesSize, int* envelopesColSize) {
if (envelopesSize == 0) return 0;
//1、先排序,首先按照第一列升序排序,若第一列的值相同,则按照第二列的值降序排序
qsort(envelopes, envelopesSize, sizeof(int*), compare);
//2、构建dp数组
int dp[envelopesSize], indexSize = 0;
dp[indexSize++] = envelopes[0][1];
for (int i = 1; i < envelopesSize; ++i) {
int num = envelopes[i][1];
if (num > dp[indexSize - 1]) dp[indexSize++] = num;
else {
//在dp中寻找第一个大于等于num的值的下标,进而替换她
int index = lower_bound(dp, indexSize, num);
dp[index] = num;
}
}
return indexSize;
}
//二分查找
int lower_bound(int* arr, int arrSize, int val)
{
int left = 0, right = arrSize - 1;
while (left <= right) {
int mid = (left + right) >> 1;
if (val < arr[mid]) right = mid - 1;
else if (val > arr[mid]) left = mid + 1;
else return mid;
}
if (arr[left] >= val) return left;
return -1;
}
//第一个参数升序 第二个参数降序
int compare(const void *a, const void *b){
int* num1 = *(int**)a;
int* num2 = *(int**)b;
if(num1[0]==num2[0]){
return num2[1] - num1[1];
} else {
return num1[0] - num2[0];
}
}
summary:
套路:遇到这种数组这种问题,经常想到以 下标i 为结尾作为的子问题,直接定义 dp【i】:为以 i 作为下标结尾的数组怎么怎么。。。。