Metric_in_Semantic_Segmentation
Metric in Semantic Segmentation
Dice Coefficient
定义:Dice系数,是一种集合相似度度量函数,通常用于计算两个样本点的相似度(值范围为[0, 1])。用于分割问题,分割最好时为1,最差为0。(可解决样本不均衡问题)
计算公式:
其中 $\left | X \cap Y \right |$ 是表示 X 和 Y 的交集(逐像素相乘后相加),$\left | X \right | $ 和 $ \left | Y \right |$ 表示其元素的个数(逐像素(Or平方)相加)。在计算的时候一般会加一个smooth,防止分母出现0
Dice loss = 1 - Dice
代码实现1(简单):
1
2
3
4
5
6
7
8# H*W,只针对二维,多类多batch分开计算
def dice_coeff(pred, target):
smooth = 1.
num = pred.size(0)
m1 = pred.view(num, -1) # Flatten
m2 = target.view(num, -1) # Flatten
intersection = (m1 * m2).sum() # 计算交集
return (2. * intersection + smooth) / (m1.sum() + m2.sum() + smooth)代码实现2(标准):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41# H*W
def dice_coeff(input: Tensor, target: Tensor, reduce_batch_first: bool = False, epsilon=1e-6):
# Average of Dice coefficient for all batches, or for a single mask
assert input.size() == target.size()
if input.dim() == 2 and reduce_batch_first:
raise ValueError(f'Dice: asked to reduce batch
but got tensor without batch dimension (shape {input.shape})')
if input.dim() == 2 or reduce_batch_first:
# torch.dot 点乘,对应元素相乘后相加,一个值,分子交集
inter = torch.dot(input.reshape(-1), target.reshape(-1))
# 分母,并集
sets_sum = torch.sum(input) + torch.sum(target)
if sets_sum.item() == 0:
sets_sum = 2 * inter
return (2 * inter + epsilon) / (sets_sum + epsilon)
else:
# compute and average metric for each batch element
dice = 0
for i in range(input.shape[0]):
dice += dice_coeff(input[i, ...], target[i, ...])
return dice / input.shape[0]
def multiclass_dice_coeff(input: Tensor, target: Tensor,
reduce_batch_first: bool = False, epsilon=1e-6):
# Average of Dice coefficient for all classes
assert input.size() == target.size()
dice = 0
for channel in range(input.shape[1]):
dice += dice_coeff(input[:, channel, ...], target[:, channel, ...],
reduce_batch_first, epsilon)
return dice / input.shape[1]
def dice_loss(input: Tensor, target: Tensor, multiclass: bool = False):
# 在调用的时候,groud-truth若是多类别,需要进行one-hot编码
# 【B,C,H,W】target and input
# Dice loss (objective to minimize) between 0 and 1
assert input.size() == target.size()
fn = multiclass_dice_coeff if multiclass else dice_coeff
return 1 - fn(input, target, reduce_batch_first=True)
Mean Intersection over Union
mIoU:Mean Intersection over Union,均交并比,为语义分割的标准度量。其计算所有类别交集和并集之比的平均值.
先验提示:
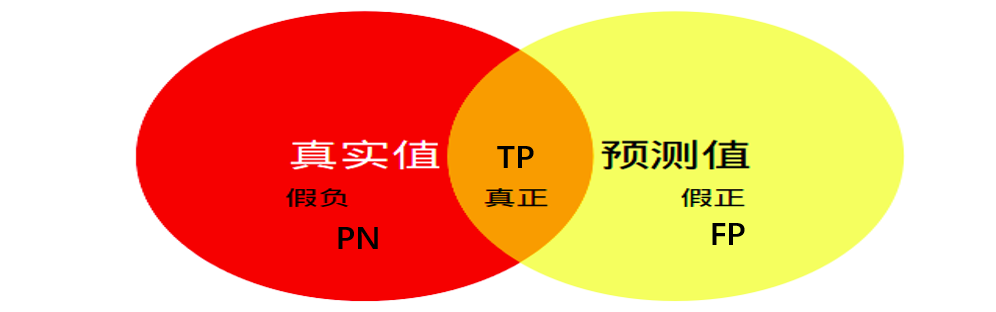
- TP(真正): 预测正确, 预测结果是正类, 真实是正类
- FP(假正): 预测错误, 预测结果是正类, 真实是负类
- FN(假负): 预测错误, 预测结果是负类, 真实是正类
- TN(真负): 预测正确, 预测结果是负类, 真实是负类 # 跟该类别无关,所以不包含在并集中
mIoU的计算:直观理解,计算两圆交集(橙色部分)与两圆并集(红色+橙色+黄色)之间的比例,理想情况下两圆重合,比例为1
计算:
先求混淆矩阵:K 分类问题就会生成 K * K 的混淆矩阵。
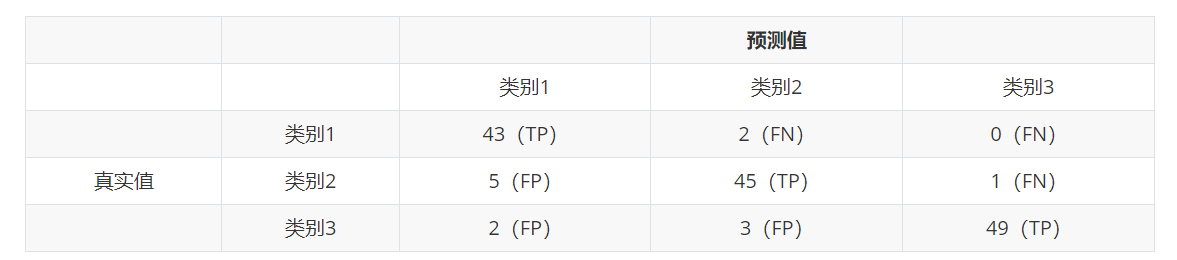
假设有150个样本数据,预测类别1,2,3各有50 个,分类结束的混淆矩阵为上:
每一行之和表示该类别的真实样本数量,每一列之和表示被预测为该类别的样本数量
第一行说明有43个属于第一类别的样本被正确预测为了第一类,有两个属于第一类别的样本被错误预测成为了第二类。
再求 mIoU:
mIoU = 混淆矩阵对角线的值 / (混淆矩阵的每一行再加上每一列,最后减去对角线上的值)
混淆矩阵: 对角线上的值的和代表分类正确的像素点个数(preb与target一致),对角线之外的其他值的和代表所有分类错误的像素的个数。
混淆矩阵矩阵中 (x, y) 位置的元素代表该张图片中真实类别为 x ,被预测为 y 的像素个数。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21# 1先求混淆矩阵
def _fast_hist(self, label_pred, label_true):
# 找出标签中需要计算的类别,去掉了背景
mask = (label_true >= 0) & (label_true < self.num_classes)
# np.bincount计算了从0到n**2-1这n**2个数中每个数出现的次数,返回值形状(n, n)
hist = np.bincount(self.num_classes * label_true[mask].astype(int) +
label_pred[mask], minlength=self.num_classes ** 2)
.reshape(self.num_classes,self.num_classes)
return hist
# 2根据混淆矩阵求mIoU
# 输入:预测值和真实值 [batch_size, H, W]
# 语义分割的任务是为每个像素点分配一个label
def ev aluate(self, predictions, gts):
for lp, lt in zip(predictions, gts):
assert len(lp.flatten()) == len(lt.flatten())
self.hist += self._fast_hist(lp.flatten(), lt.flatten())
# miou
# 每个类别 iou
iou = np.diag(self.hist) / (self.hist.sum(axis=1) + self.hist.sum(axis=0) np.diag(self.hist))
# 取平均值
miou = np.nanmean(iou)
常用求mIoU代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41# 输入 pred,target 【B,H,W】
# 第一种方式 比较合适我理解
def iou_mean(pred, target, n_classes = 1):
# n_classes :the number of classes in your dataset,not including background
# for mask and ground-truth label, not probability map
ious = [] #每个类别的 IoU
iousSum = 0
pred = pred.view(-1)
target = target.view(-1)
# Ignore IoU for background class ("0")
for cls in range(1, n_classes+1):
pred_inds = pred == cls
target_inds = target == cls
# Cast to long to prevent overflows
intersection = (pred_inds[target_inds]).long().sum().data.cpu().item()
union = pred_inds.long().sum().data.cpu().item()
+ target_inds.long().sum().data.cpu().item() - intersection
if union == 0:
ious.append(float('nan')) # If there is no ground truth, do not include in evaluation
else:
ious.append (float(intersection) / float(max(union, 1)))
iousSum += float(intersection) / float(max(union, 1))
return iousSum/n_classes # mIoU
# 第二种方式
# 'K' classes, output and target sizes are N or N * L or N * H * W, each value in range 0 to K - 1.
def intersectionAndUnion(output, target, K, ignore_index=255):
assert output.ndim in [1, 2, 3]
assert output.shape == target.shape
output = output.reshape(output.size).copy()
target = target.reshape(target.size)
output[np.where(target == ignore_index)[0]] = ignore_index
intersection = output[np.where(output == target)[0]]
area_intersection, _ = np.histogram(intersection, bins=np.arange(K + 1))
area_output, _ = np.histogram(output, bins=np.arange(K + 1))
area_target, _ = np.histogram(target, bins=np.arange(K + 1))
area_union = area_output + area_target - area_intersection
ious = area_intersection / area_union+epsilon # 是一个array,代表每个类别的IoU
mIoU = np.nanmean(ious) # mIoU
Dice和IoU的联系:
其中在 Dice 中 $\left | X \cap Y \right |$ 就是 TP,$\left | X \right |$ 假设是ground-truth的话就是 FN+TP,$\left | Y \right |$ 假设是预测的 mask的话就是 TP+FP:
得到:
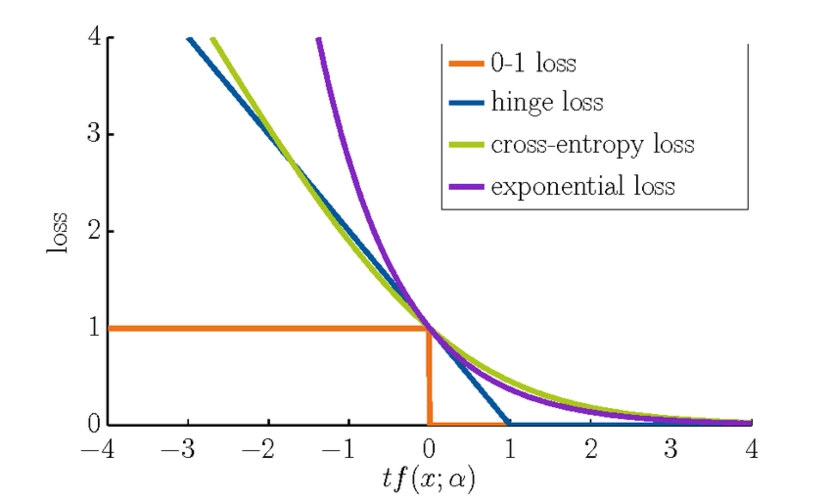
根据在【0,1】值域中的函数图像,可以发现:
- IoU和Dice同时为0,同时为1;这很好理解,就是全预测正确和全部预测错误
- 在相同的预测情况下,可以发现Dice给出的评价会比IoU高一些